ECON 0150 | Economic Data Analysis

The economist’s data analysis skillset.

Part 5.1 | Categorical Controls

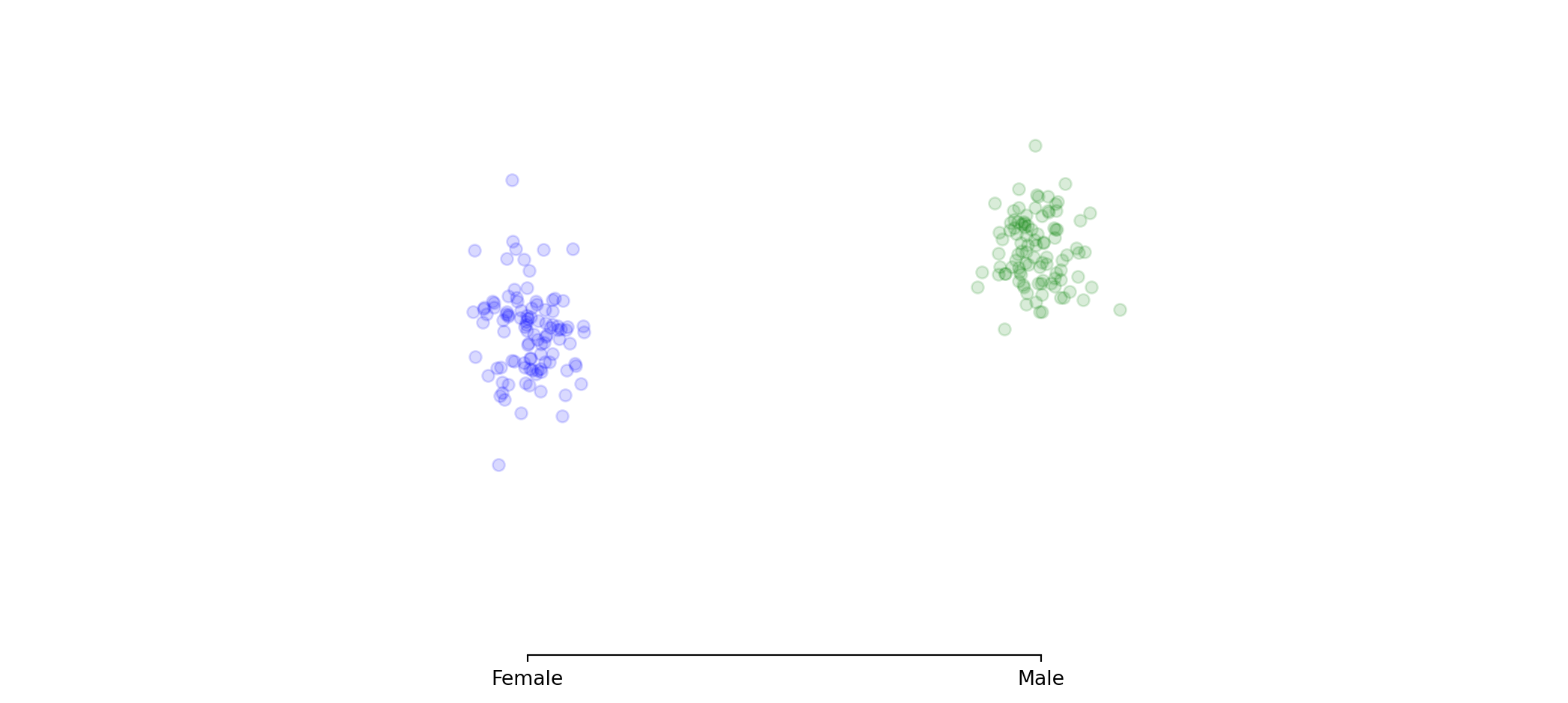
GLM: The Gender Wage Gap

Lets use the general linear model to test for differences in wages by gender.

Questions:

• Is there a wage gap between male / female?
• Are returns to education different between male / female?

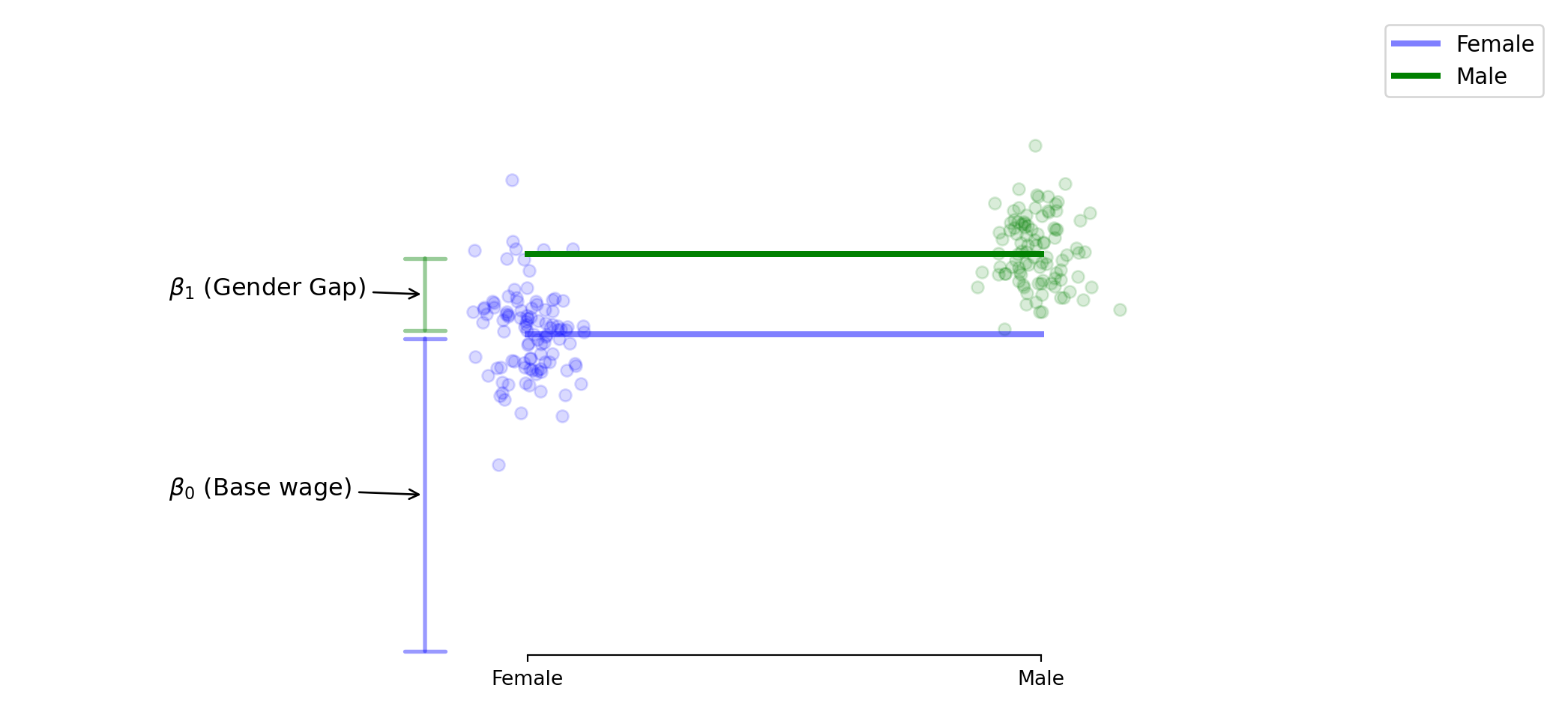
Model 1: Basic Gender Wage Gap

The simplest model with just a gender indicator.

Model 1: Basic Gender Wage Gap

The simplest model with just a gender indicator.

\[\text{Wage} = \beta_0 + \beta_1 \times \text{Male} + \varepsilon\]

Model 1: Basic Gender Wage Gap

The simplest model with just a gender indicator.

\[\text{Wage} = \beta_0 + \beta_1 \times \text{Male} + \varepsilon\]

• β₀ is the average wage for females
• β₁ represents the gender wage gap - the additional wage for males
• We often call a Categorical Control variable like this a “Fixed Effect”

Model 1: The Code

Implementing the basic gender gap model

import statsmodels.formula.api as smf

# Fit the model with just the male indicator
model1 = smf.ols('INCLOG10 ~ MALE', data=data).fit()
print(model1.summary().tables[1])

• If β₁ > 0, this is evidence of a difference in income by gender
• There are many possible explainations for this gap
• What if the gap is related to some other factor (eg. education)?

Model 2: Education + Gender Wage Gap

Adding education as a control variable.

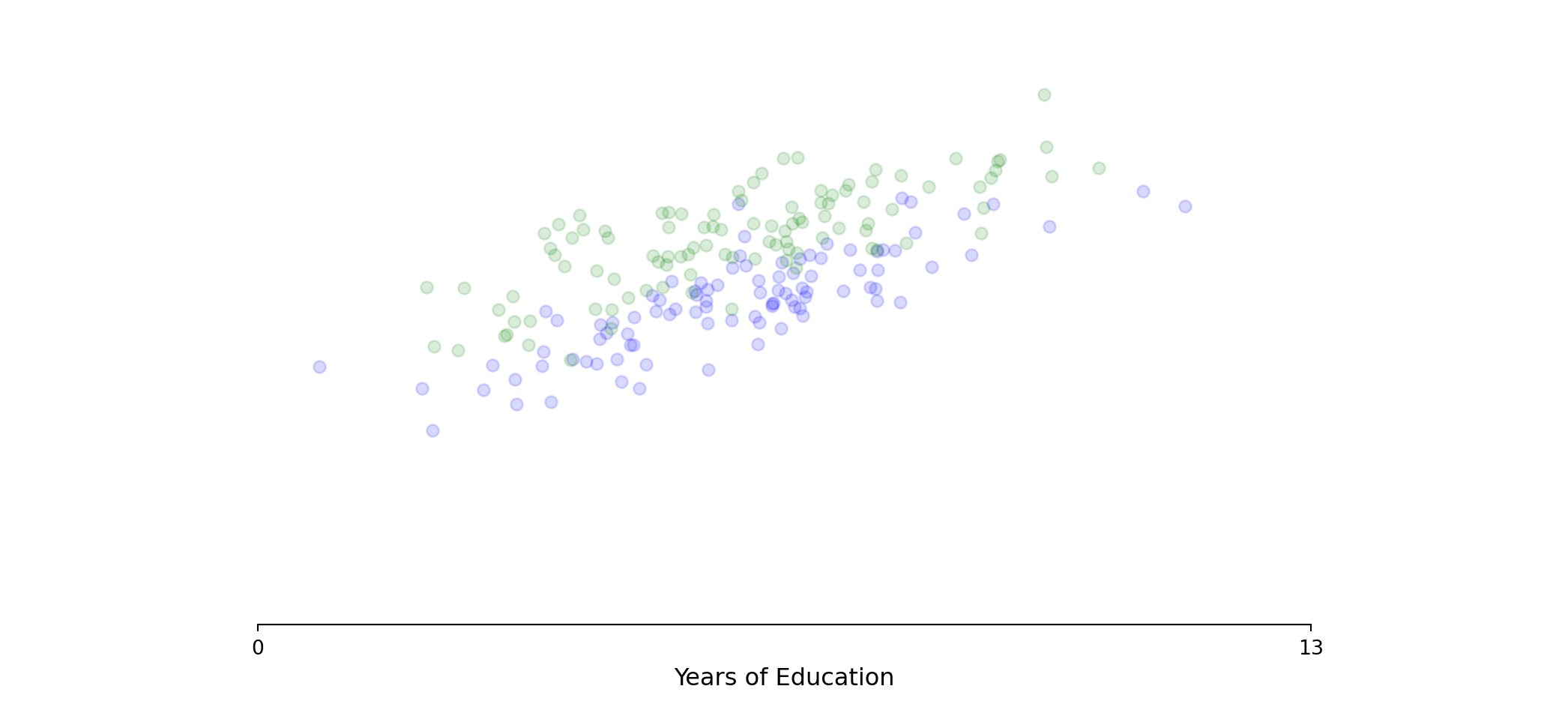
Model 2: Education + Gender Wage Gap

Adding education as a control variable.

Model 2: Education + Gender Wage Gap

Adding education as a control variable.

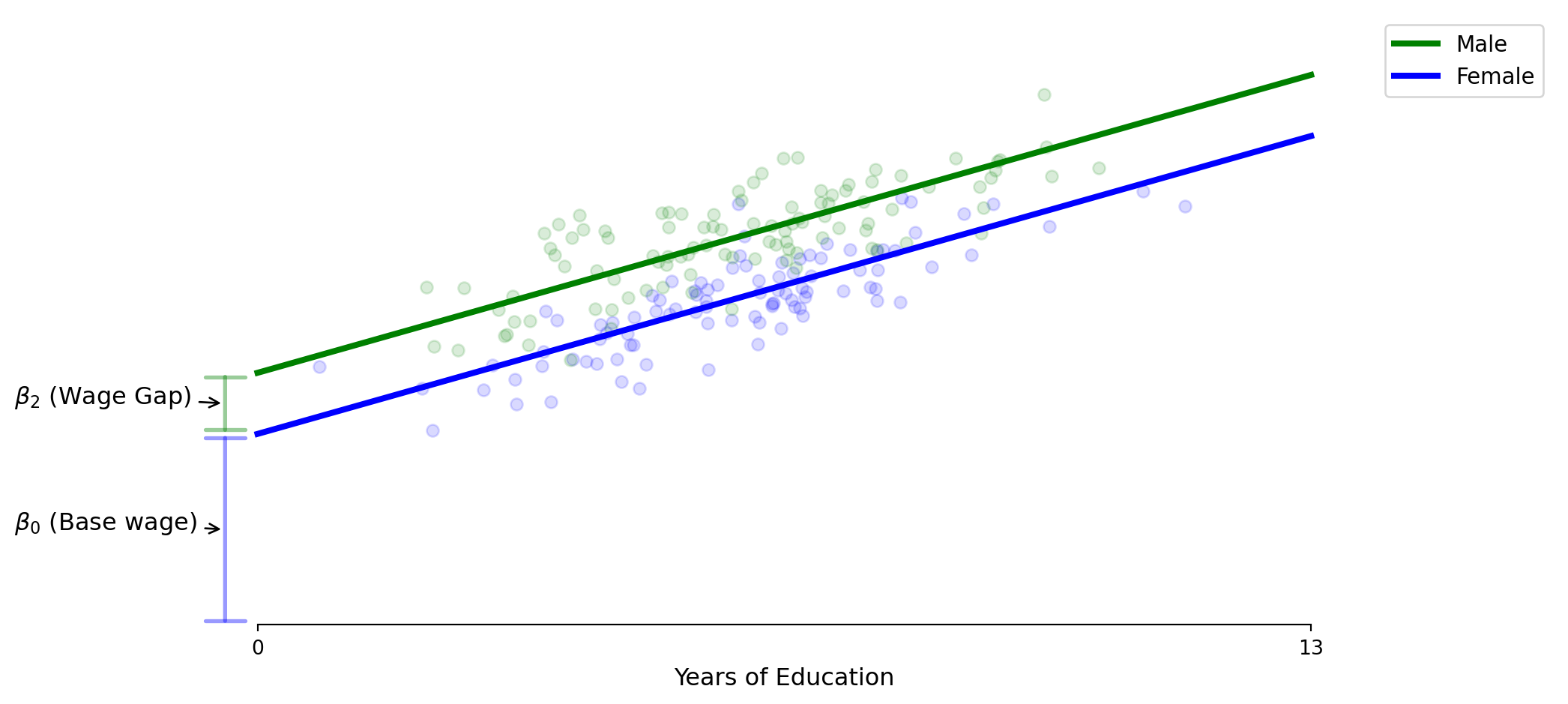
\[\text{Wage} = \beta_0 + \beta_1 \times \text{Education} + \beta_2 \times \text{Male} + \varepsilon\]

Model 2: Education + Gender Wage Gap

Adding education as a control variable.

\[\text{Wage} = \beta_0 + \beta_1 \times \text{Education} + \beta_2 \times \text{Male} + \varepsilon\]

> β₀ is the base wage for those with no post-middle school education

> β₂ represents the gender wage gap - added to the intercept for males only

> model assumes parallel lines - same returns to education (β₁) for everyone

Model 2: The Code

Implementing the gender fixed effect model

import statsmodels.formula.api as smf

# Fit the model with male indicator
model2 = smf.ols('INCLOG10 ~ EDU + MALE', data=data).fit()
print(model2.summary().tables[1])

• If β₂ > 0, there is evidence of a gender wage gap.

ECON 0150 | Economic Data Analysis

The economist’s data analysis skillset.

Part 5.2 | Interaction Models

Model 3: Different Returns to Education

What if education benefits genders differently?

Model 3: Different Returns to Education

What if education benefits genders differently?

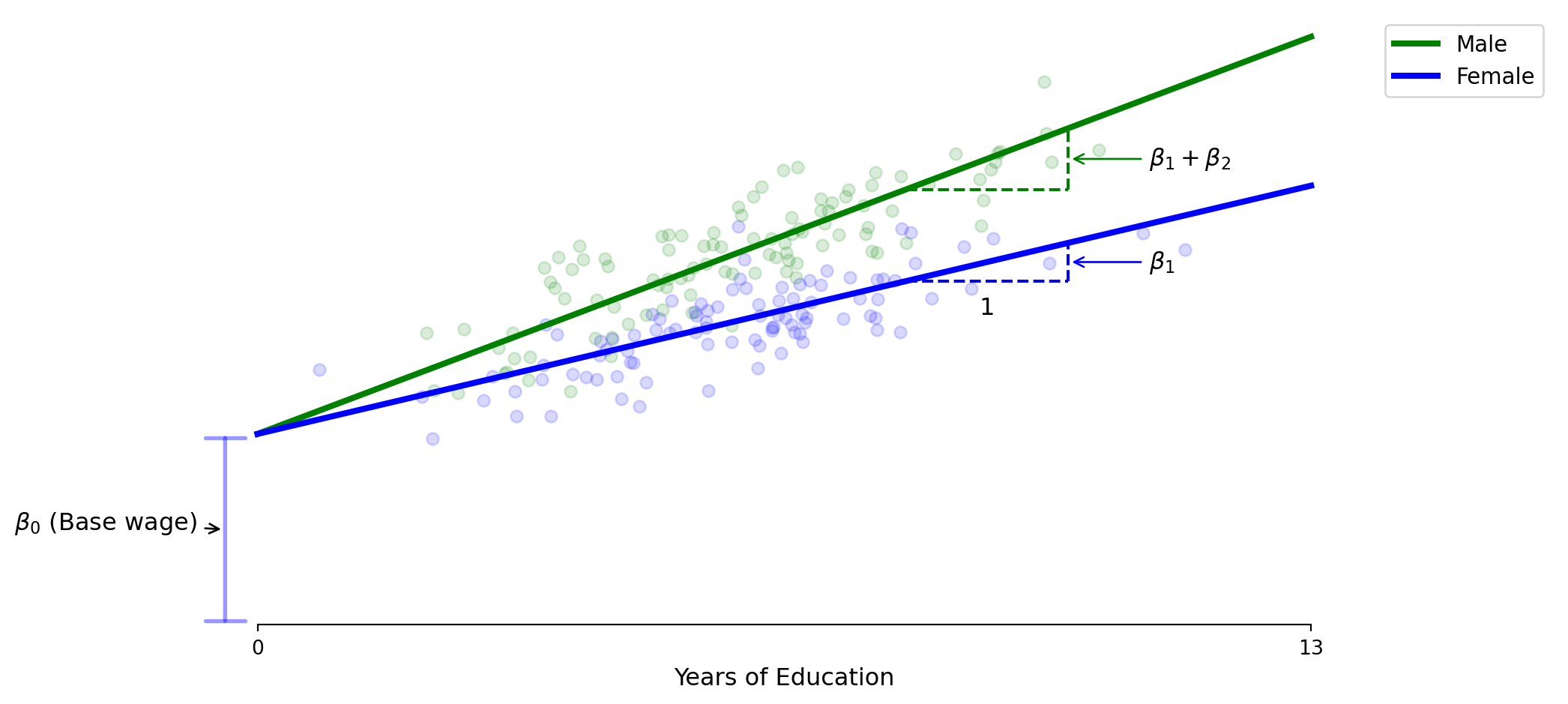
\[\text{Wage} = \beta_0 + \beta_1 \times \text{Education} + \beta_2 \times \text{Education} \times \text{Male} + \varepsilon\]

Model 3: Different Returns to Education

What if education benefits genders differently?

\[\text{Wage} = \beta_0 + \beta_1 \times \text{Education} + \beta_2 \times \text{Education} \times \text{Male} + \varepsilon\]

• β₁ represents the female return to education.
• β₂ represents the additional male return to education - this changes the slope
• Male education effect is β₁ + β₂, creating diverging wage paths

Model 3: The Code

Implementing the education-gender interaction model

# Fit model with interaction between education and sex
model3 = smf.ols('INCLOG10 ~ EDU + EDU:MALE', data=data).fit()
print(model3.summary().tables[1])

• If β₂ > 0 and significant, male return to education is higher
• This model assumes same baseline (intercept) for both genders

Model 4: Full Gender Difference Model

Combining fixed effects and interactions

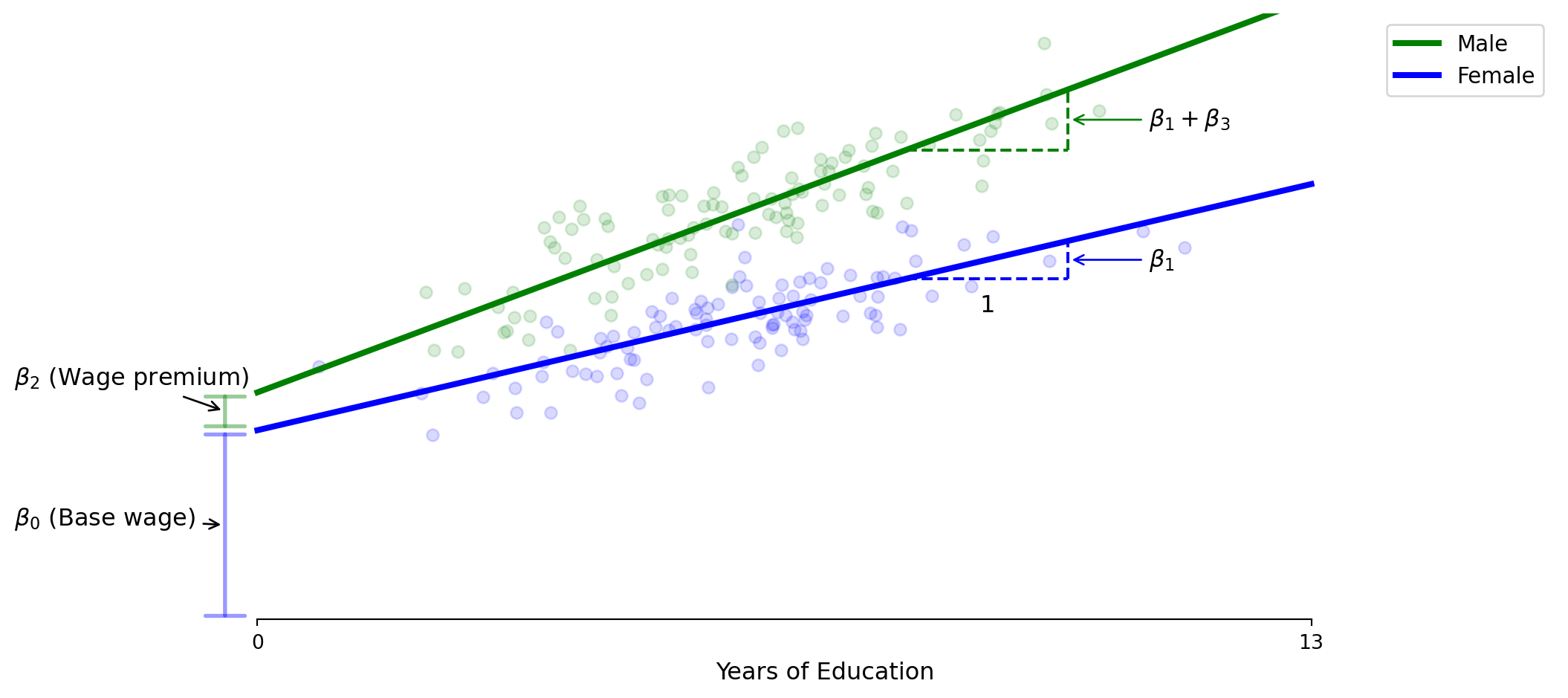
\[\text{Wage} = \beta_0 + \beta_1 \times \text{Education} + \beta_2 \times \text{Male} + \beta_3 \times \text{Education} \times \text{Male} + \varepsilon\]

Model 4: Full Gender Difference Model

Combining fixed effects and interactions

\[\text{Wage} = \beta_0 + \beta_1 \times \text{Education} + \beta_2 \times \text{Male} + \beta_3 \times \text{Education} \times \text{Male} + \varepsilon\]

• β₀ = base wage
• β₂ = initial wage gap (at zero education)
• β₁ = female returns to education
• β₃ = male education return premium

Model 4: The Code

Implementing the full gender difference model

# Fit full model with both sex indicator and interaction
model4 = smf.ols('INCLOG10 ~ EDU + MALE + EDU:MALE', data=data).fit()
print(model4.summary().tables[1])

> allows for differences in both baseline wages and educational returns

Comparison of Models

Different models answer different questions

Model 1: Fixed Effect

• Question: “Is there a gender wage gap?”

Model 2: Fixed Effect with Control

• Question: “Is there a gender wage gap controling for education?”

Model 3: Interaction Only

• Question: “Are there differences in returns to education?”

Model 4: Fixed Effect and Interaction

• Question: “Does the gender wage gap vary with education level?”

Key Takeaways

General linear model for analyzing group differences

Part 5.1 | Categorical Controls (‘Fixed Effects’)

• Captures level differences between groups

Part 5.2 | Interactions

• Capture differences in slopes

Model Choice should be guided by your research question