ECON 0150 | Economic Data Analysis

The economist’s data analysis workflow.

Part 4.4 | The Problem of Timeseries

Timeseries Analysis

We often want to model relationships through time.

Data related in time has a special problem:

• Observations are related to their past values (autocorrelation).

• This violates Assumption 4: Independence.

Timeseries Analysis: Autocorrelation

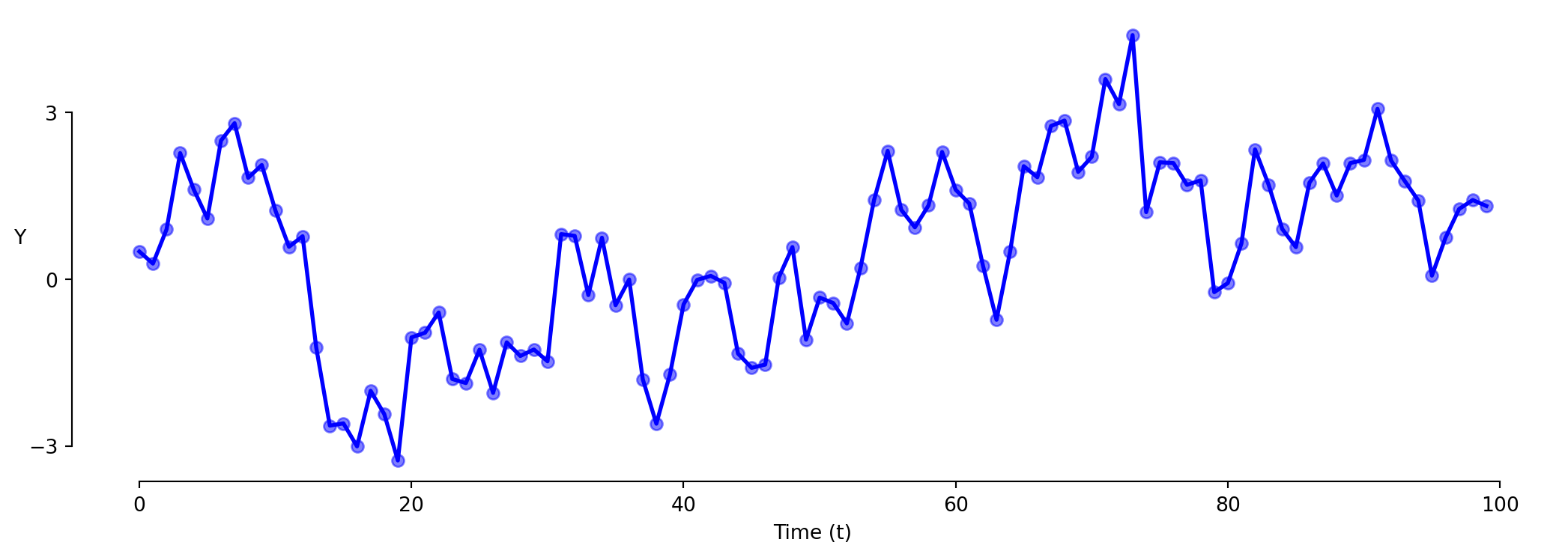
We can check whether values in timeseries are related to their own past values.

A Lag Plot shows the value today (\(t\)) against the value yesterday (\(t-1\)).

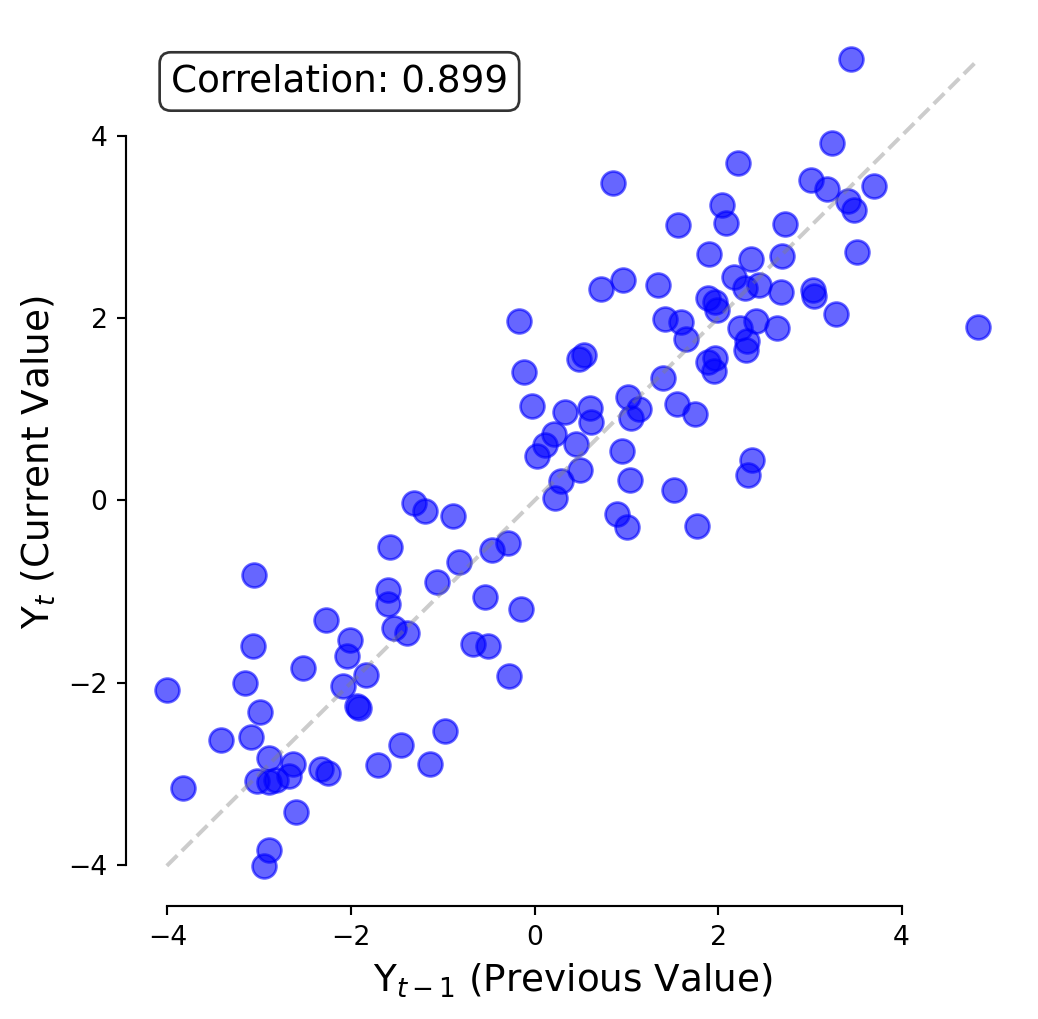
> autocorrelation tells us today’s value depends on yesterday’s value

Timeseries: Model 1 (Levels)

The standard approach has problems with time series.

\[\text{Y} = \beta_0 + \beta_1 \cdot \text{t} + \varepsilon\]

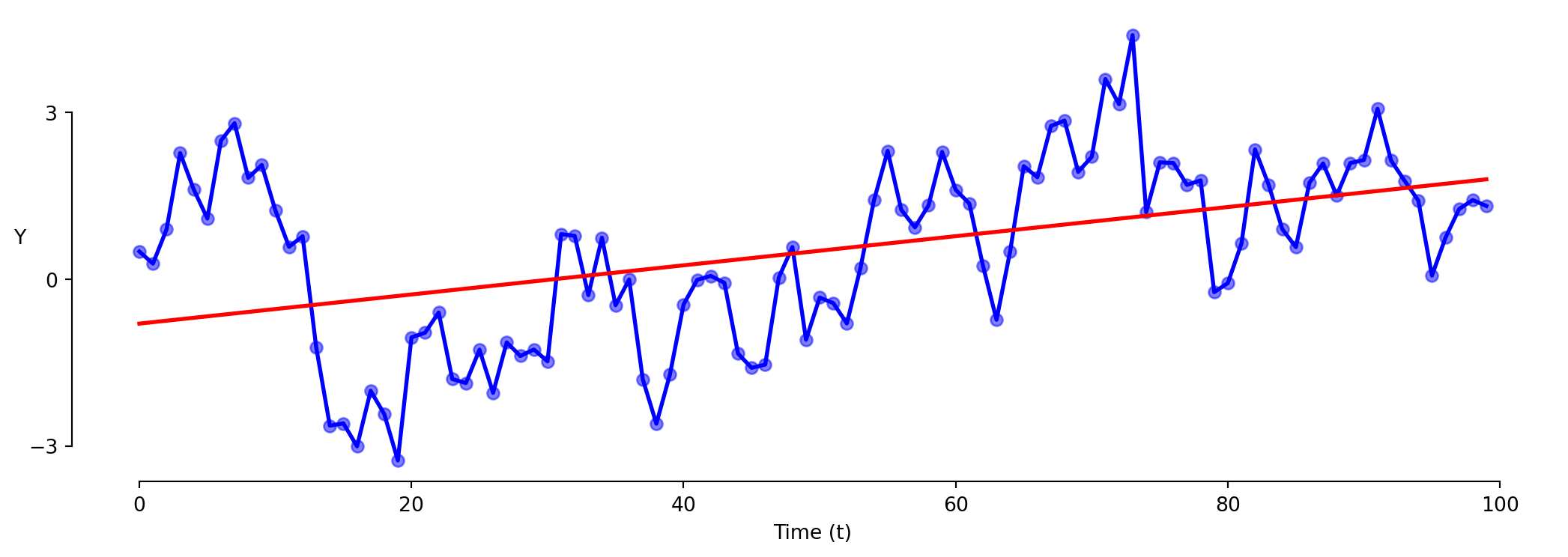
Timeseries: Model 1 (Levels)

The standard approach has problems with time series.

\[\text{Y} = \beta_0 + \beta_1 \cdot \text{t} + \varepsilon\]

> you can see it will often be wrong in the same direction repeatedly

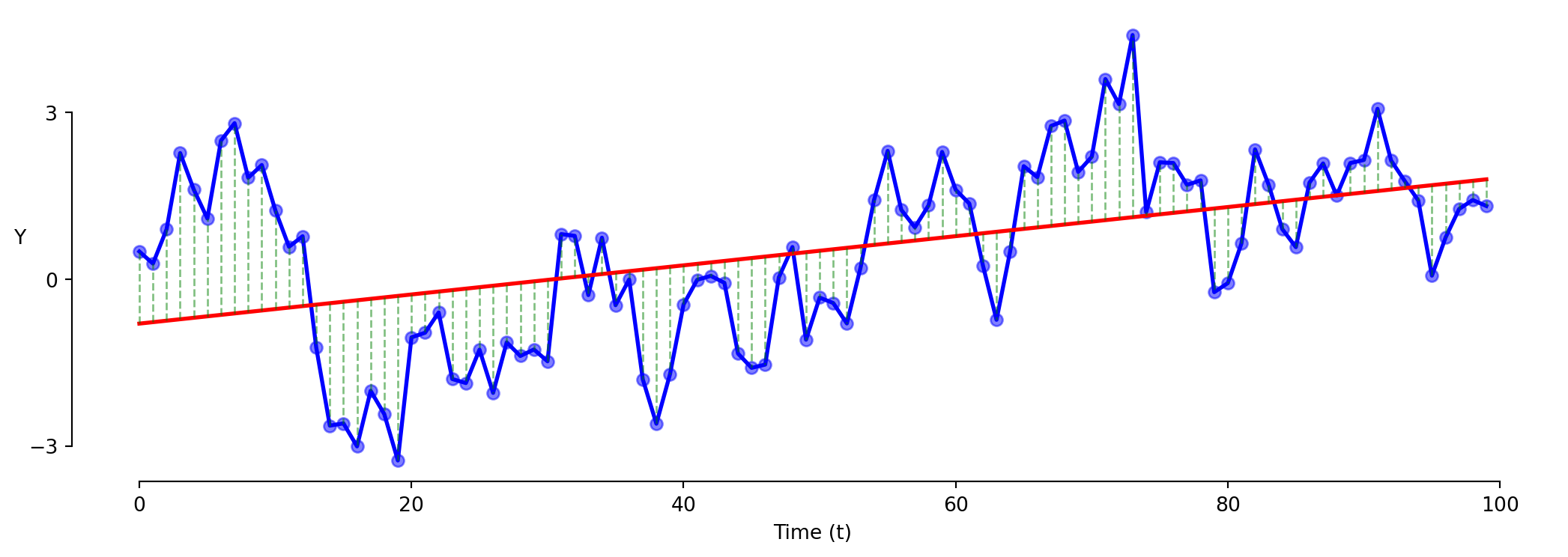
Timeseries: Model 1 (Levels)

GLM’s confidence levels requres that the error terms are independent.

\[\text{Y} = \beta_0 + \beta_1 \cdot \text{t} + \varepsilon\]

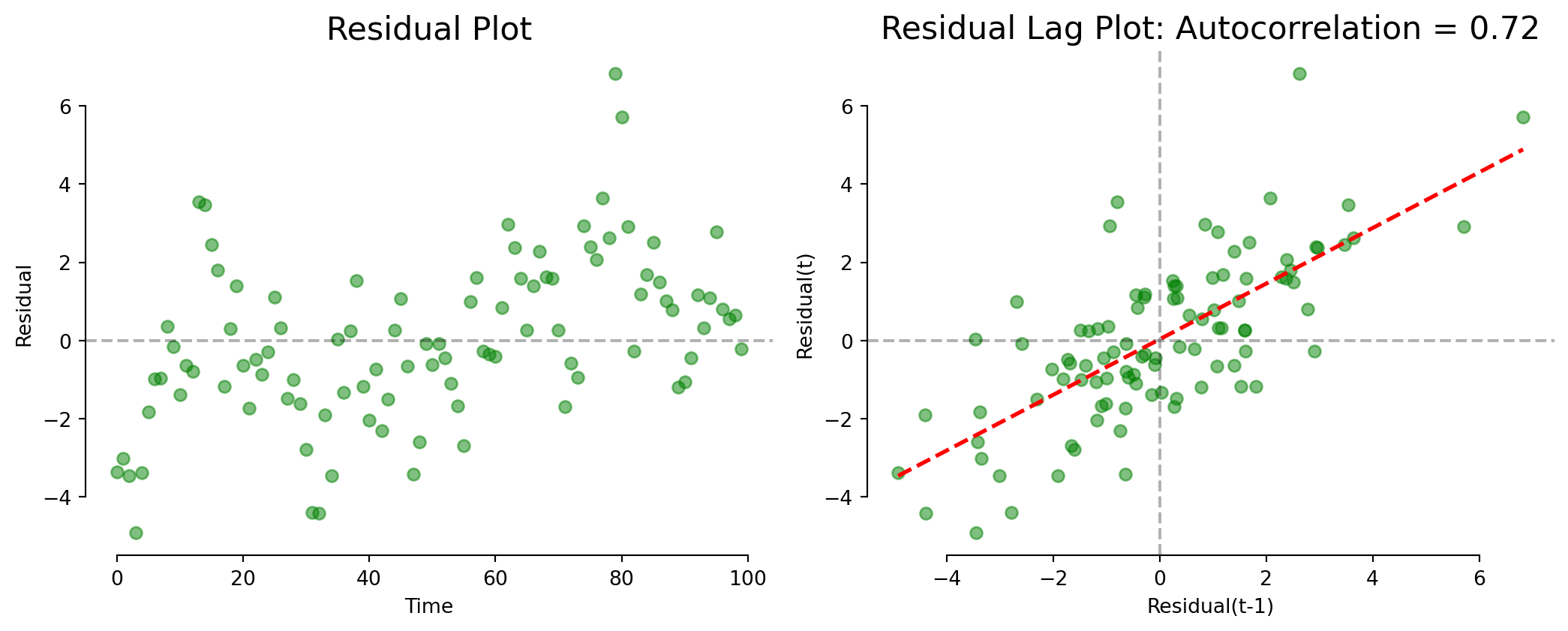
> this ‘levels’ model shows strong patterns in residuals (autocorrelation)

Exercise 4.4 | Model 1 (Levels)

Examine a levels model of the relationship between GDP and unemployment.

\[\text{Y} = \beta_0 + \beta_1 \times \text{t} + \varepsilon\]

# 1. Fit the levels model
model1 = smf.ols('gdp ~ unemployment', data=data).fit()
print(model1.summary().tables[1])

Timeseries: Model 2 (First Differences)

We can fix some issues of autocorrelation by looking at changes instead of levels.

\[\Delta \text{Y}_t = \text{Y}_t - \text{Y}_{t-1}\]

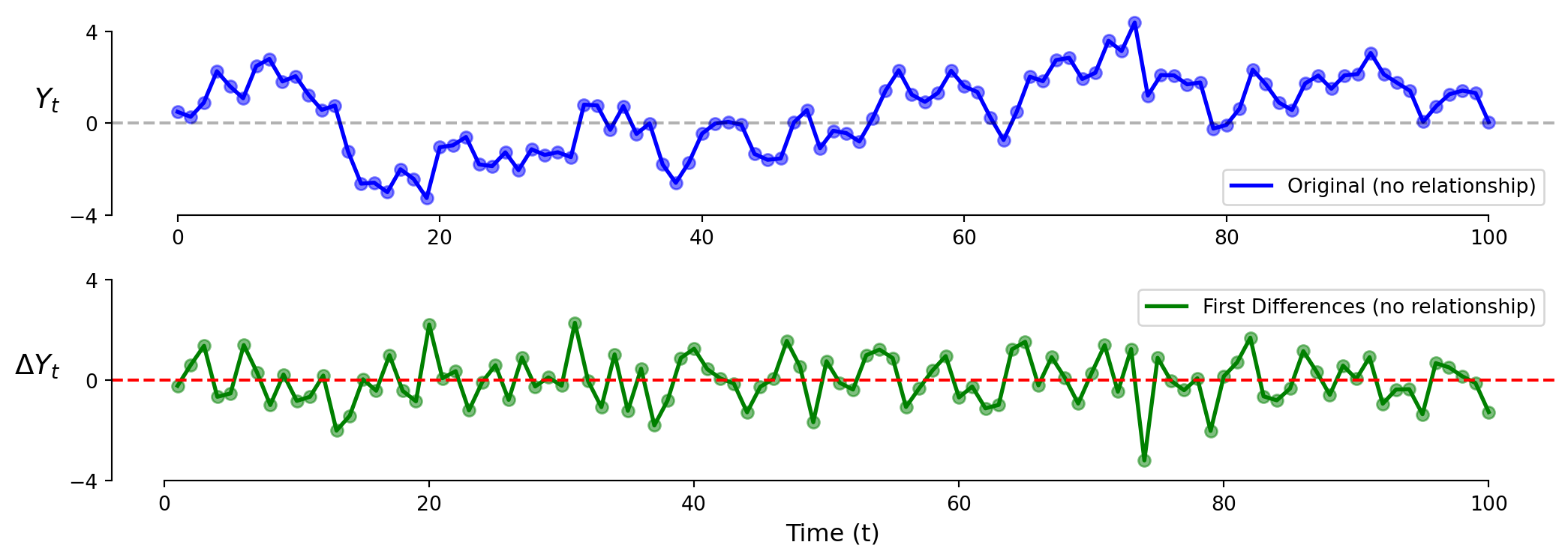
> differences (correctly in this case) shows no relationship

> what would first differences look like if there WAS a positive trend?

Timeseries: Model 2 (First Differences)

What would first differences look like if there WAS a positive trend?

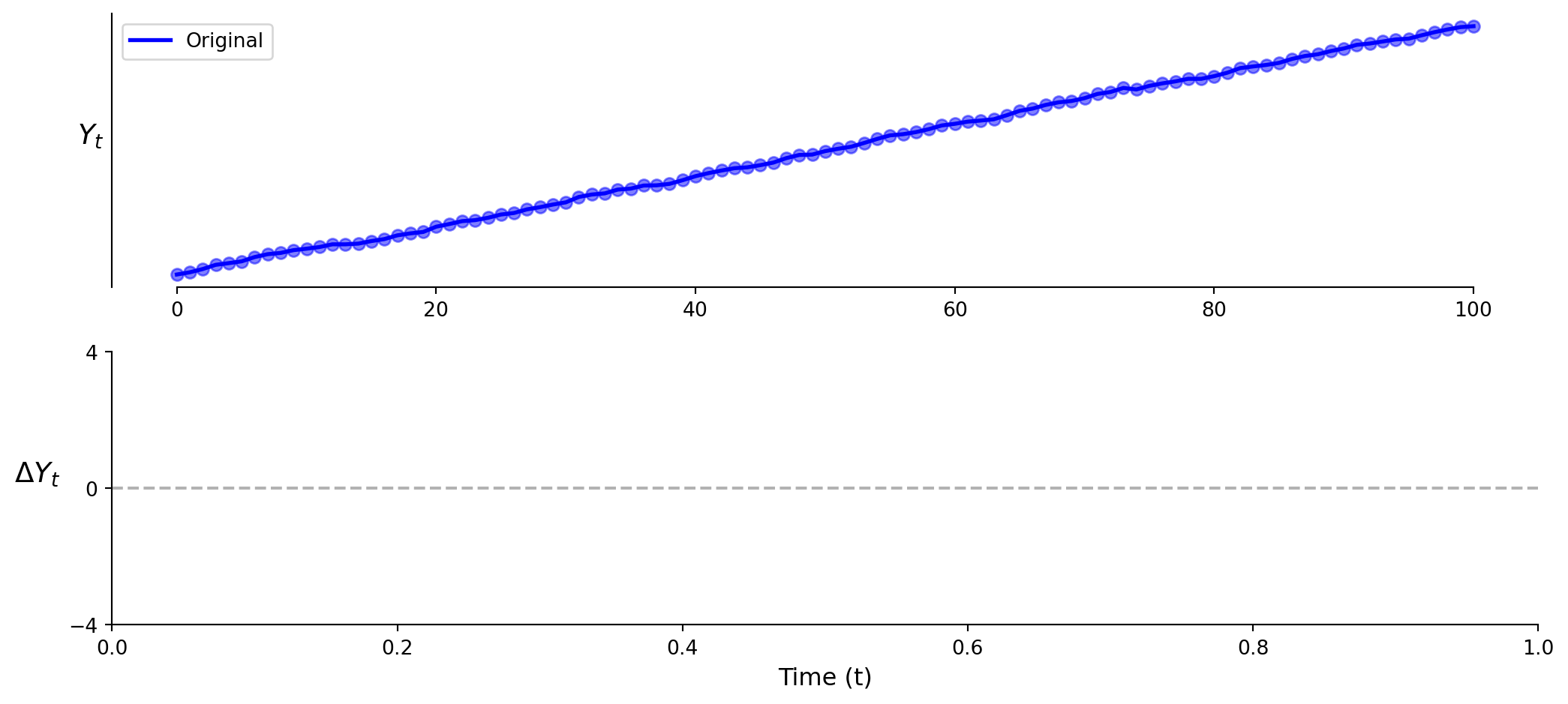
Timeseries: Model 2 (First Differences)

What would first differences look like if there WAS a positive trend?

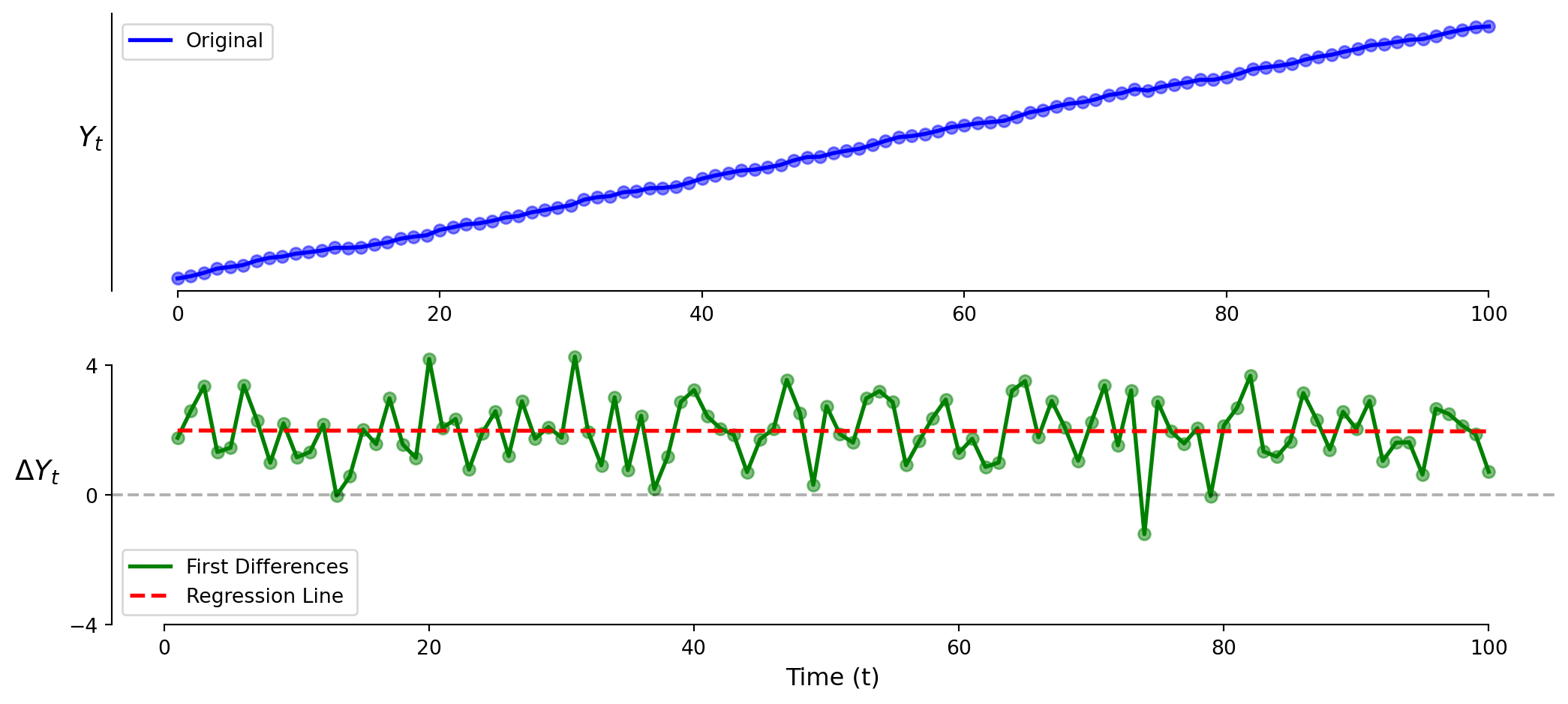
> the vertical intercept \(\beta_0\) is positive!

> the slope coefficient \(\beta_1\) is zero!

Timeseries: Model 2 (First Differences)

First differences reduces but does not eliminate the problem of autocorrelation.

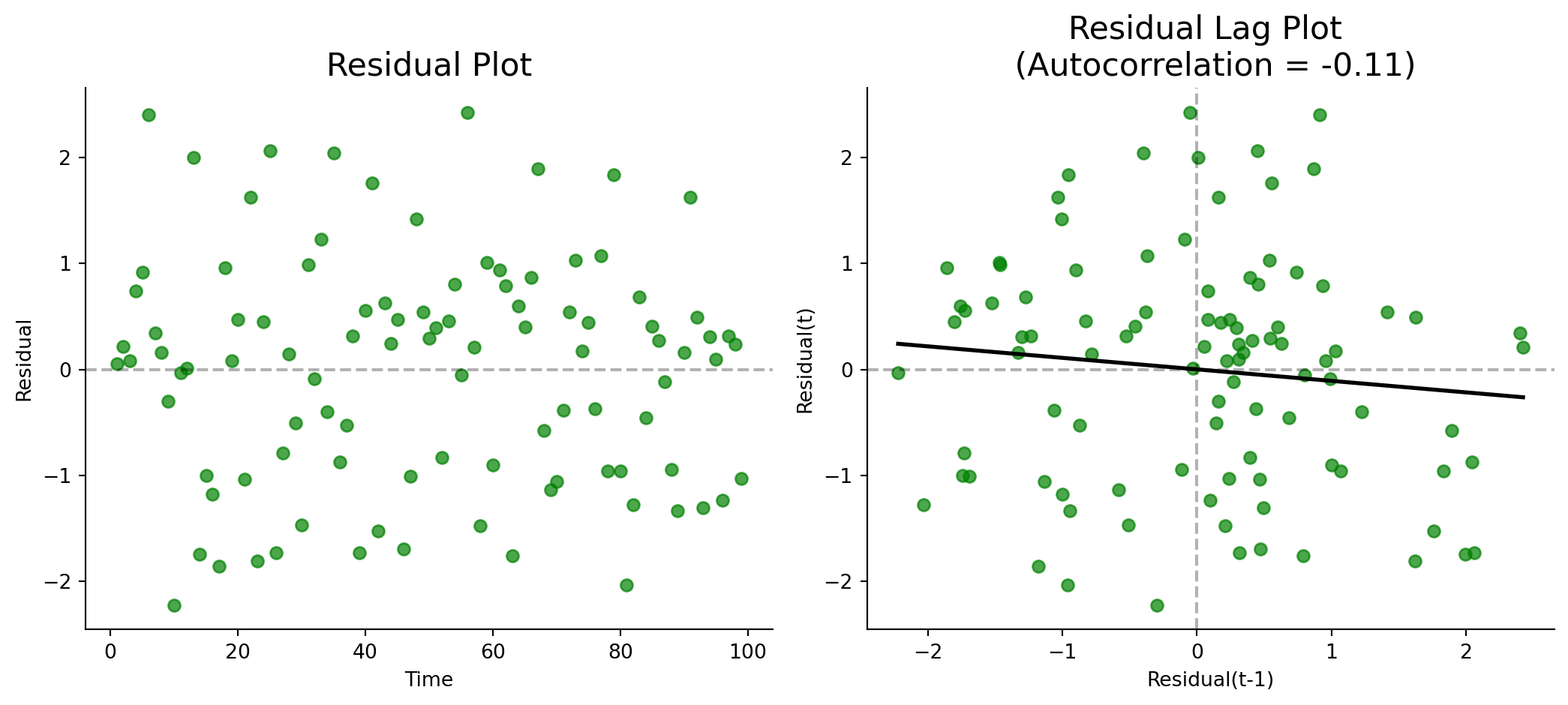
Exercise 4.4 | Model 2

Examine a first difference model of the relationship between GDP and unemployment.

# Step 1. Create first differences variables
data['gdp_diff'] = data['gdp'].diff()
data['unemployment_diff'] = data['unemployment'].diff() 

# Step 2. Drop the first row which has NaN due to differencing
data = data.dropna()

# Step 3. Fit the differences model
model2 = smf.ols('gdp_diff ~ unemployment_diff', data=data).fit()
print(model2.summary().tables[1])

Timeseries: Model 3 (Double First Differences)

Sometimes we want to measure how two variables move together.

\[\Delta \text{Y}_t = \beta_0 + \beta_1 \times \Delta \text{X}_t + \varepsilon_t\]

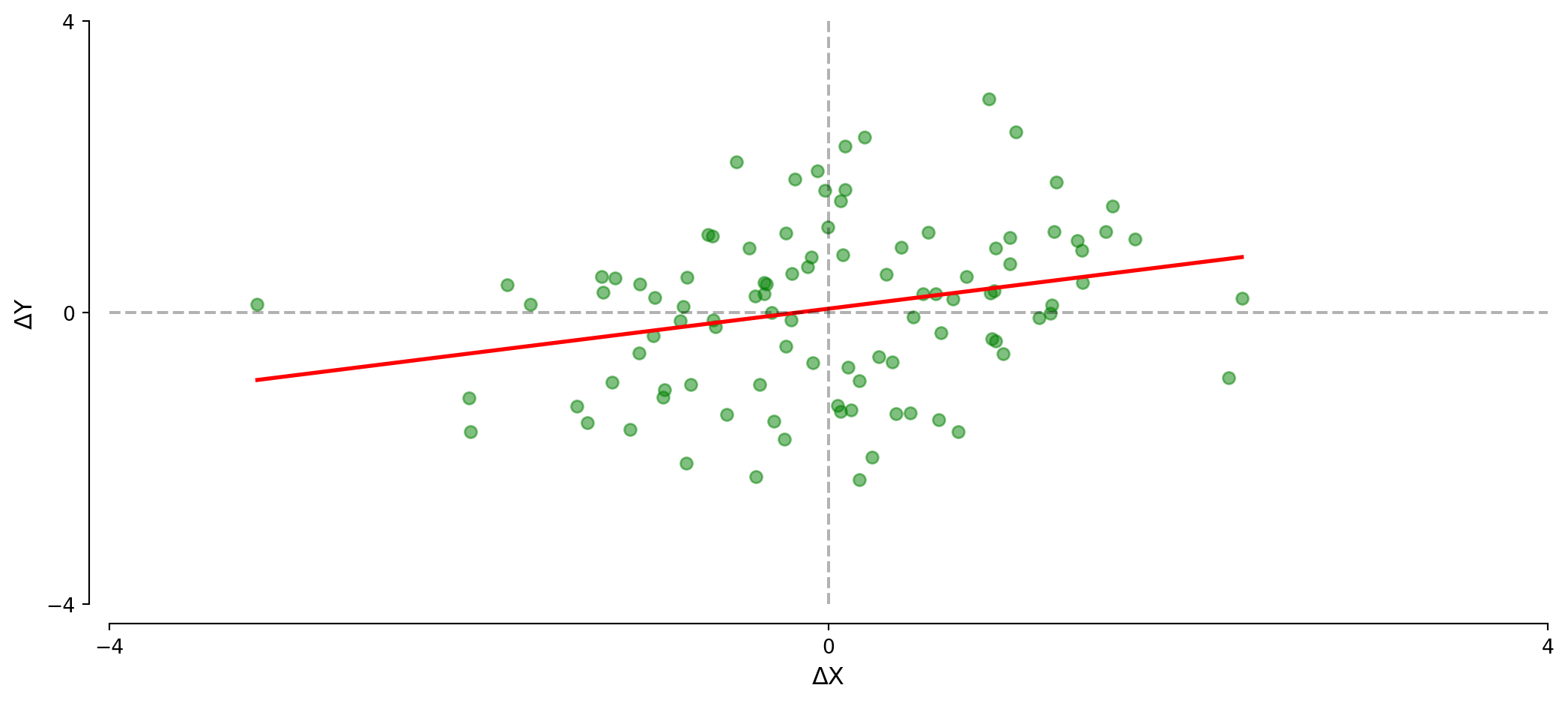
Timeseries: Model 3 (Double First Differences)

Relating changes in X to changes in Y.

\[\Delta \text{Y}_t = \beta_0 + \beta_1 \times \Delta \text{X}_t + \varepsilon_t\]

• Further reduces serial correlation in the error terms.

• \(\beta_0\) captures time trend in \(Y\)

• \(\beta_1\) captures the short-term relationship between variables.

• Clear interpretation: how do changes in X relate to changes in Y?

Exercise 4.4 | Model 3

Examine a double first difference model of the relationship between GDP and unemployment.

# Step 1. Create first differences variables
data['gdp_diff'] = df['gdp'].diff()
df['unemployment_diff'] = df['unemployment'].diff()

# Drop the first row which has NaN due to differencing
data = data.dropna()

# Fit the differences model
model3 = smf.ols('gdp_diff ~ unemployment_diff', data=data).fit()
print(model3.summary())

> \(\beta_1\) now represents the short-term relationship between changes in X and Y

Timeseries: Model 4 (Growth Rates)

Proportional changes provide interpretable coefficients:

\[g_Y = \frac{\text{Y}_t - \text{Y}_{t-1}}{\text{Y}_{t-1}} = \frac{\Delta \text{Y}_t}{\text{Y}_{t-1}}\]

Timeseries: Model 4 (Growth Rates)

Proportional changes provide interpretable coefficients:

\[g_Y = \frac{\text{Y}_t - \text{Y}_{t-1}}{\text{Y}_{t-1}} = \frac{\Delta \text{Y}_t}{\text{Y}_{t-1}}\]

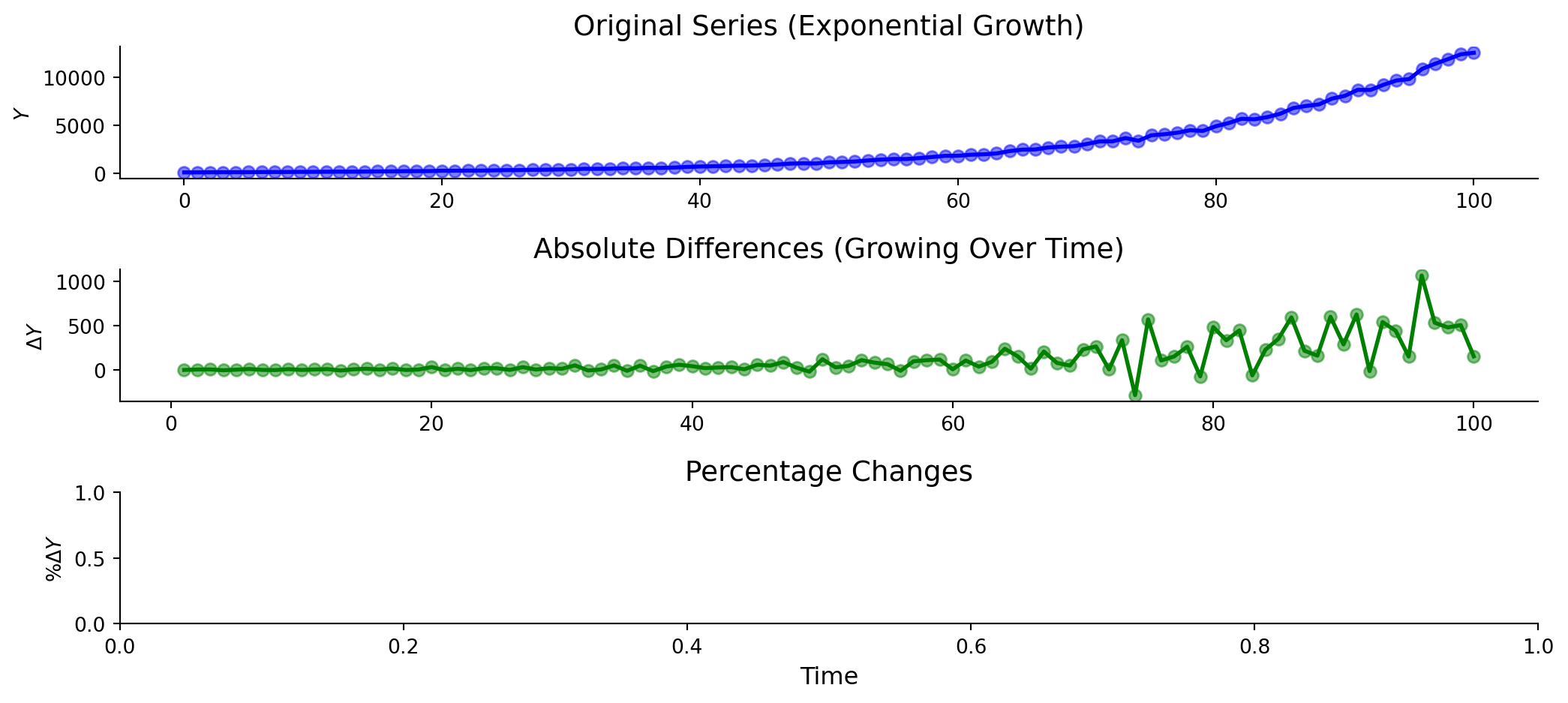
Timeseries: Model 4 (Growth Rates)

Proportional changes provide interpretable coefficients:

\[g_Y = \frac{\text{Y}_t - \text{Y}_{t-1}}{\text{Y}_{t-1}} = \frac{\Delta \text{Y}_t}{\text{Y}_{t-1}}\]

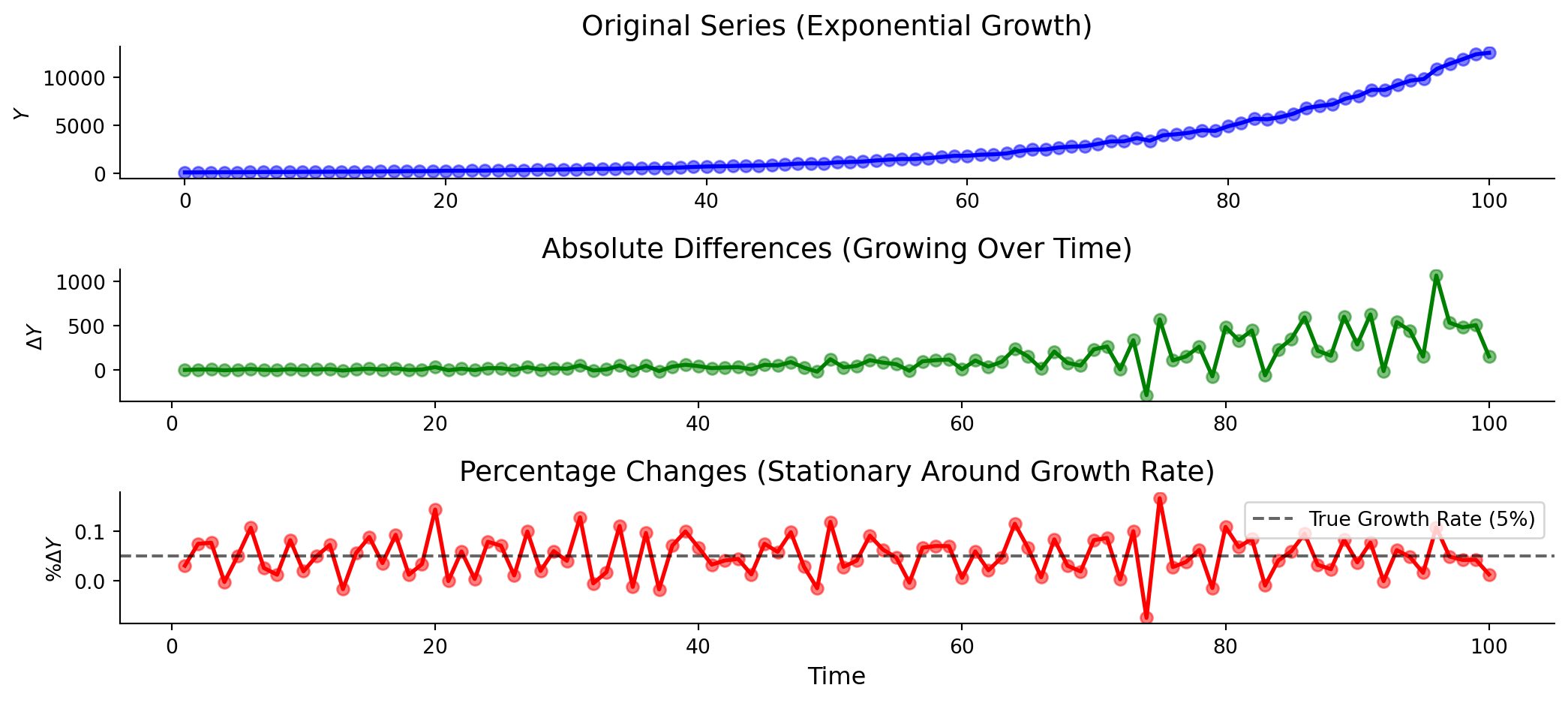
Timeseries: Model 4 (Growth Rates)

Is the growth in Y related to the growth in X?

\[g_Y = \beta_0 + \beta_1 \times g_X + \varepsilon_t\]

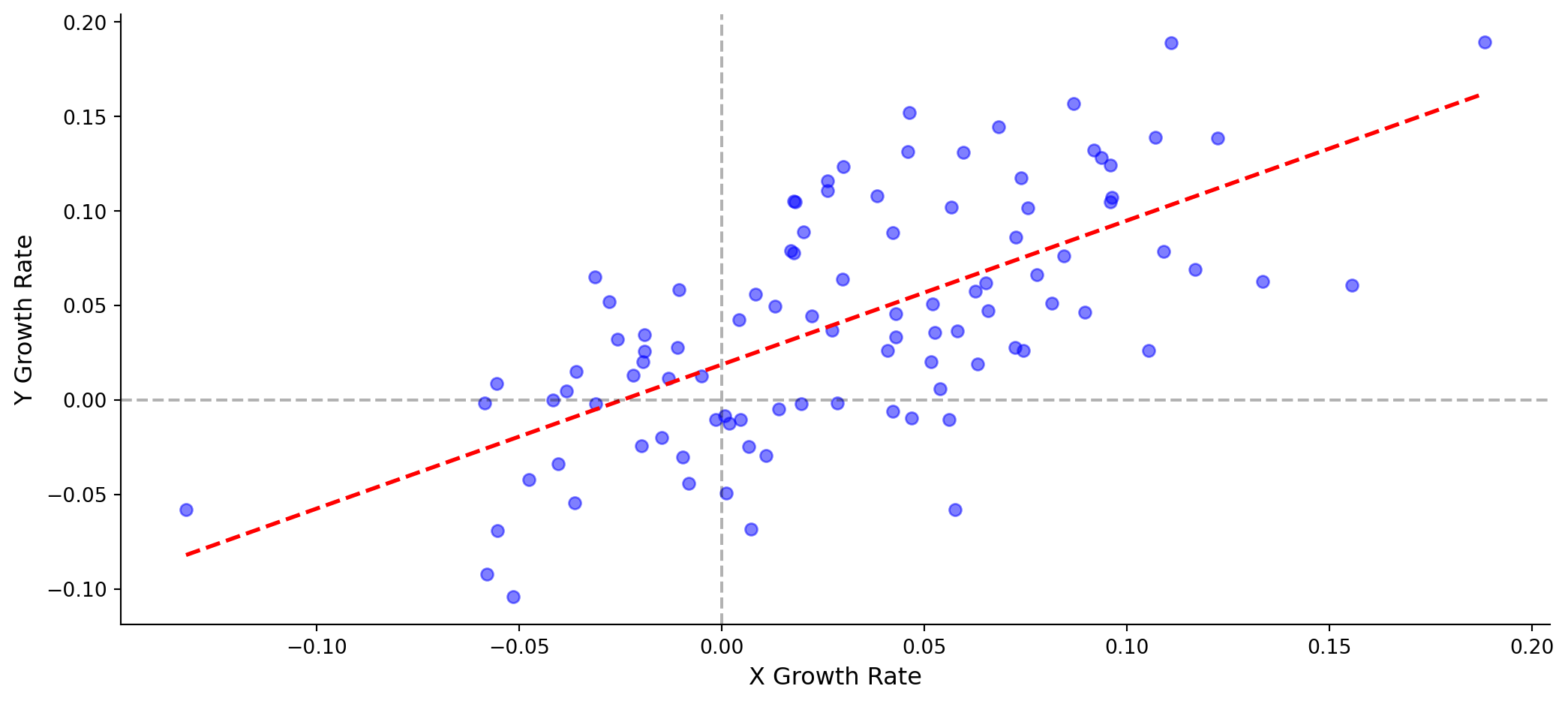
Timeseries: Model 4 (Growth Rates)

Is the growth in Y related to the growth in X?

\[g_Y = \beta_0 + \beta_1 \times g_X + \varepsilon_t\]

Growth rate models have the advantages of first differences and can scale better.

• This is natural for variables with exponential growth.

• \(\beta_0\) is Y’s baseline growth rate.

• \(\beta_1\) is how Y’s growth responds to a 1 percentage point increase in X’s growth.

Exercise 4.4 | Model 4

Examine a growth rates model of the relationship between GDP and unemployment.

# Step 1. Calculate growth rates (percentage changes)
data['gdp_growth'] = data['gdp'].pct_change() # in percentage points
data['unemployment_growth'] = data['unemployment'].pct_change()

# Step 2. Drop rows with NaN values
data = data.dropna()

# Step 3. Fit the growth rate model
model4 = smf.ols('gdp_growth ~ unemployment_growth', data=data).fit()
print(model4.summary())

> \(\beta_1\) is now expressed in percentage point terms