ECON 0150 | Economic Data Analysis

The economist’s data analysis workflow.

Part 4.3 | Categorical Predictors

General Linear Model

… a flexible approach to run many statistical tests.

The Linear Model: \(y_i = \beta_0 + \beta_1 x_i + \varepsilon_i\)

• \(\beta_0\) is the intercept (value of \(\bar{y}\) when x = 0)
• \(\beta_1\) is the slope (change in y per unit change in x)
• \(\varepsilon_i\) is the error term (random noise around the model)

OLS Estimation: Minimizes \(\sum_{i=1}^n \varepsilon_i^2\)

GLM: Intercept Model

A one-sample t-test is a horizontal line model.

\[Temperature = \beta_0 + \varepsilon\]

> the intercept \(\beta_0\) is the estimated mean temperature

> the p-value is the probability of seeing \(\beta_0\) if the null is true

GLM: Intercept + Slope

A regression is a test of relationships.

\[\text{WaitTime} = \beta_0 + \beta_1 \text{MinutesAfterOpening} + \epsilon\]

> the intercept parameter \(\beta_0\) is the estimated temperature at 0 on the horizontal

> the slope parameter \(\beta_1\) is the estimated change in y for a 1 unit change in x

> the p-value is the probability of seeing parameter (\(\beta_0\) or \(\beta_1\)) if the null is true

GLM: City Greenspace and Temperature

Q. Is temperature lower in neighborhoods with more green space?

Q. Does temperature change as we move out on the horizontal axis?

\[Temperature = \beta_0 + \beta_1 \cdot HighGreen + \varepsilon\]

> the GLM performs a t-test on \(\beta_1\), whether the difference is significant

GLM: City Greenspace and Temperature

Q. Does temperature change as we move out on the horizontal axis?

\[Temperature = \beta_0 + \beta_1 \cdot HighGreen + \varepsilon\]

How would we interpret \(\beta_0\) here?

> \(\beta_0\) is the mean temperature in (\(x=0\)) low green space cities (22.03°C)

GLM: City Greenspace and Temperature

Q. Does temperature change as we move out on the horizontal axis?

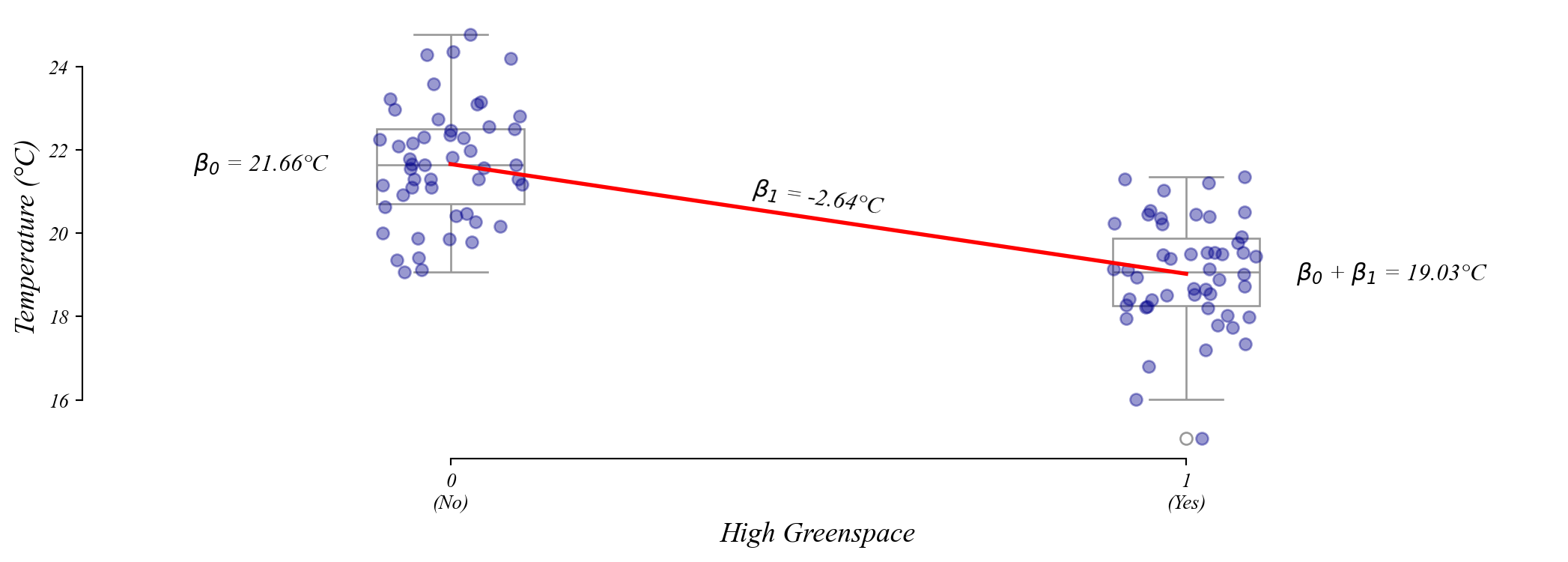
\[Temperature = \beta_0 + \beta_1 \cdot HighGreen + \varepsilon\]

How would we interpret \(\beta_1\) here?

> Cities with Green Space (x=1) have a temperature that is lower by \(\beta_1\)

> ie. a one unit increase in \(x\) changes temperature by \(\beta_1\)

GLM: City Greenspace and Temperature

Q. Does temperature change as we move out on the horizontal axis?

> p-value on \(\beta_1\): probability of a slope as extreme as \(\beta_1\) under the null dist

Exercise: Neighborhood Income and Pollution

Do low-income neighborhoods face higher pollution levels?

Step 1: Summarize the data

# Visualize Binary Predictor
sns.scatterplot(data, x='low_income', y='pollution')
plt.xticks([0,1], labels=['No', 'Yes'])

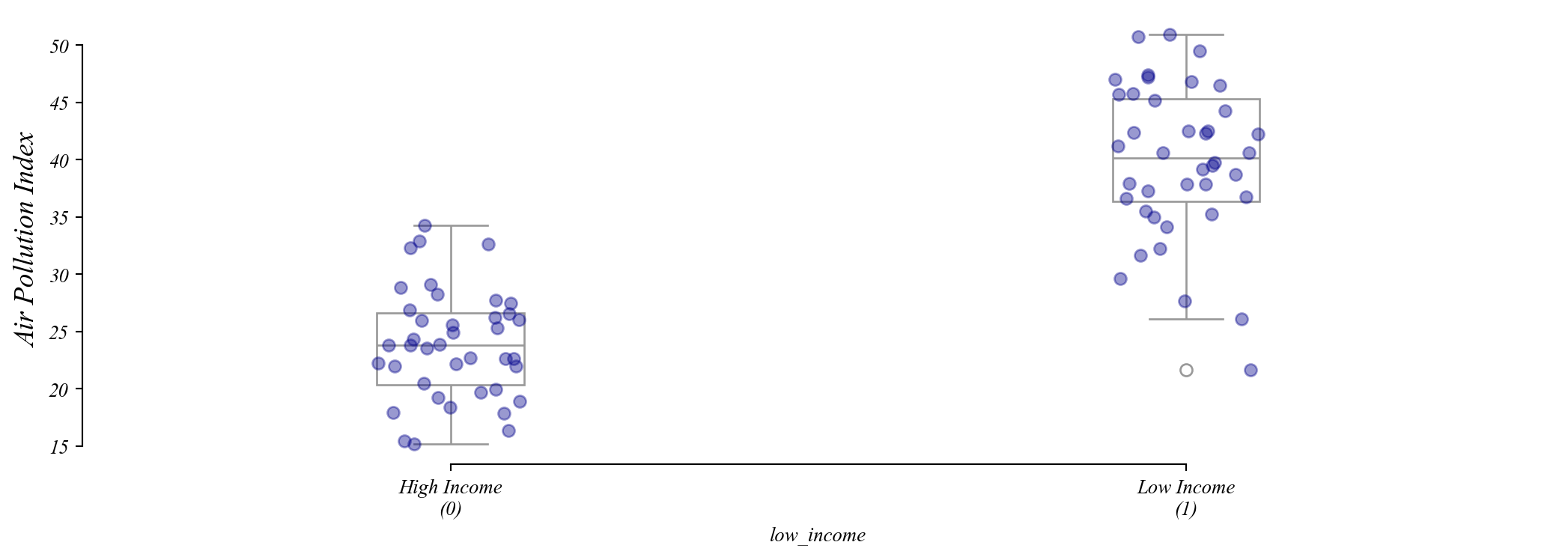
Exercise: Neighborhood Income and Pollution

Do low-income neighborhoods face higher pollution levels?

Step 2: Build a model

\[Pollution = \beta_0 + \beta_1 \cdot LowIncome + \varepsilon\]

Exercise: Neighborhood Income and Pollution

Do low-income neighborhoods face higher pollution levels?

Step 3: Estimate the model

# Model: y = b + mx
model = smf.ols('pollution ~ low_income', data).fit() # Intercept is included by default
print(model.summary().tables[1])

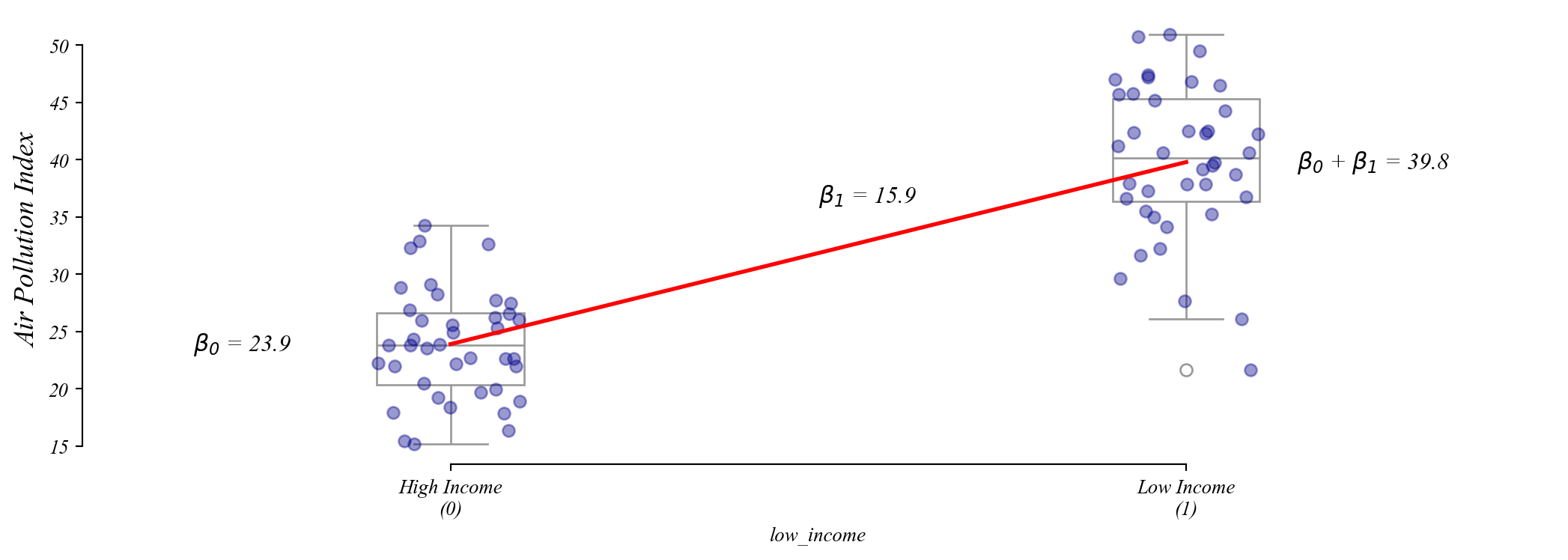
• \(\beta_0\) = Mean pollution in high-income areas (23.9)

• \(\beta_1\) = Additional pollution in low-income areas (15.9)

Exercise: Neighborhood Income and Pollution

Do low-income neighborhoods face higher pollution levels?

Step 4: Check the residuals

sns.scatterplot(x=model.predict(), y=model.resid, alpha=0.5)
plt.axhline(y=0, color='red', linestyle='-')
plt.xlabel('Fitted Values')
plt.ylabel('Residuals')

Exercise: Neighborhood Income and Pollution

Do low-income neighborhoods face higher pollution levels?

Step 5: Interpret and communicate the findings

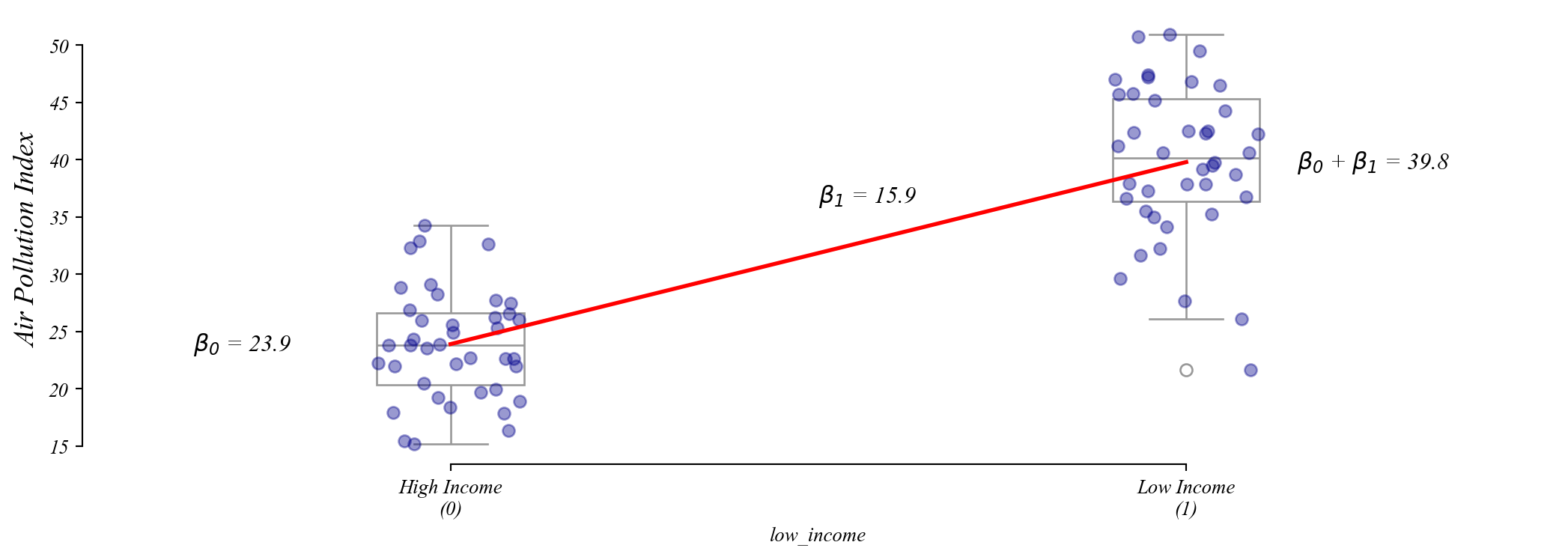
> A significant positive \(\beta_1\) suggests environmental quality differences between neighborhoods

GLM: Summary (so far)

GLM’s unified framework for testing statistical models

One-Sample T-Test: Continuous outcome variable (\(y\)) with only an intercept

\[y = \beta_0 + \varepsilon\]

Relationships: Continuous outcome variable (\(y\)) with a continuous predictor (\(x\))

\[y = \beta_0 + \beta_1 x + \varepsilon\]

Two-Sample T-Test: Continuous outcome variable (\(y\)) with a dummy (\(Group\))

\[y = \beta_0 + \beta_1 \cdot Group + \varepsilon\]

Multiple Regression: Adding control variables to isolate relationships

> all use the same OLS framework and interpretation of coefficients and p-values