ECON 0150 | Economic Data Analysis

The economist’s data analysis skillset.


Part 4.3 | Model Residuals and Diagnostics

General Linear Model

… a flexible approach to run many statistical tests.

The Linear Model: \(y_i = \beta_0 + \beta_1 x_i + \varepsilon_i\)

  • \(\beta_0\) is the intercept (value of \(\bar{y}\) when x = 0)
  • \(\beta_1\) is the slope (change in y per unit change in x)
  • \(\varepsilon_i\) is the error term (random noise around the model)

OLS Estimation: Minimizes \(\sum_{i=1}^n \varepsilon_i^2\)

GLM: Intercept Model

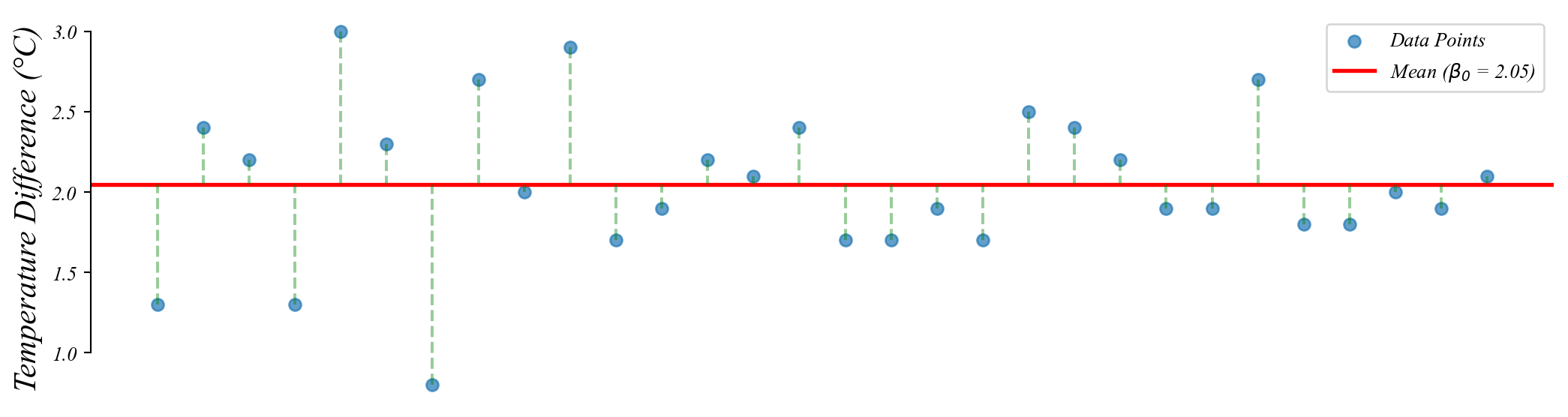
A one-sample t-test is a horizontal line model.

\[Temperature = \beta_0 + \varepsilon\]

> the intercept \(\beta_0\) is the estimated mean temperature

> the p-value is the probability of seeing \(\beta_0\) if the null is true

GLM: Intercept + Slope

A regression is a test of relationships.

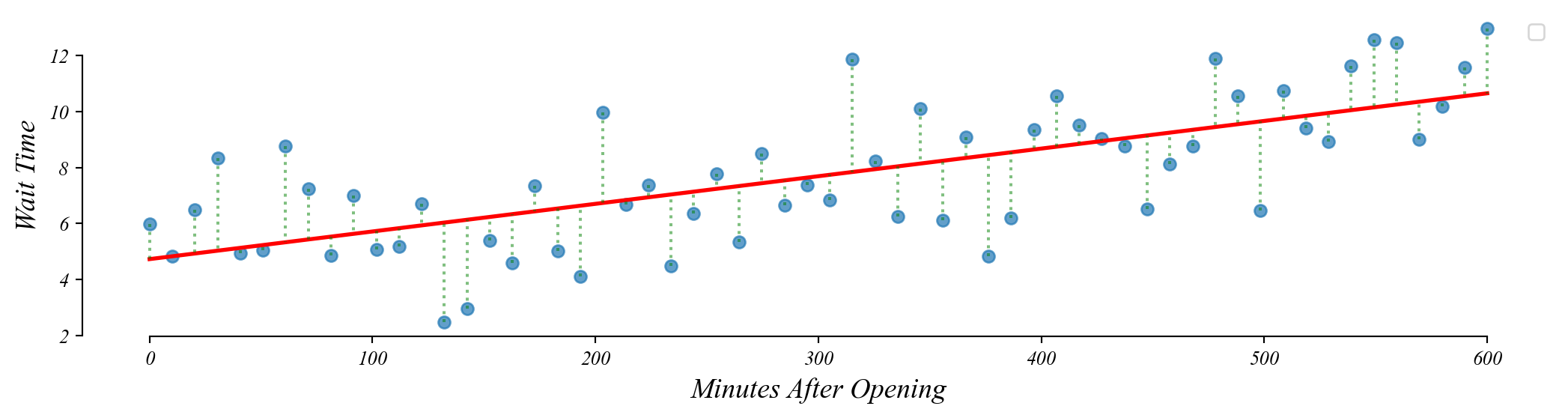
\[\text{WaitTime} = \beta_0 + \beta_1 \text{MinutesAfterOpening} + \epsilon\]

> the intercept parameter \(\beta_0\) is the estimated temperature at 0 on the horizontal

> the slope parameter \(\beta_1\) is the estimated change in y for a 1 unit change in x

> the p-value is the probability of seeing parameter (\(\beta_0\) or \(\beta_1\)) if the null is true

GLM: Intercept + Slope

Which model do you think offers better predictions?

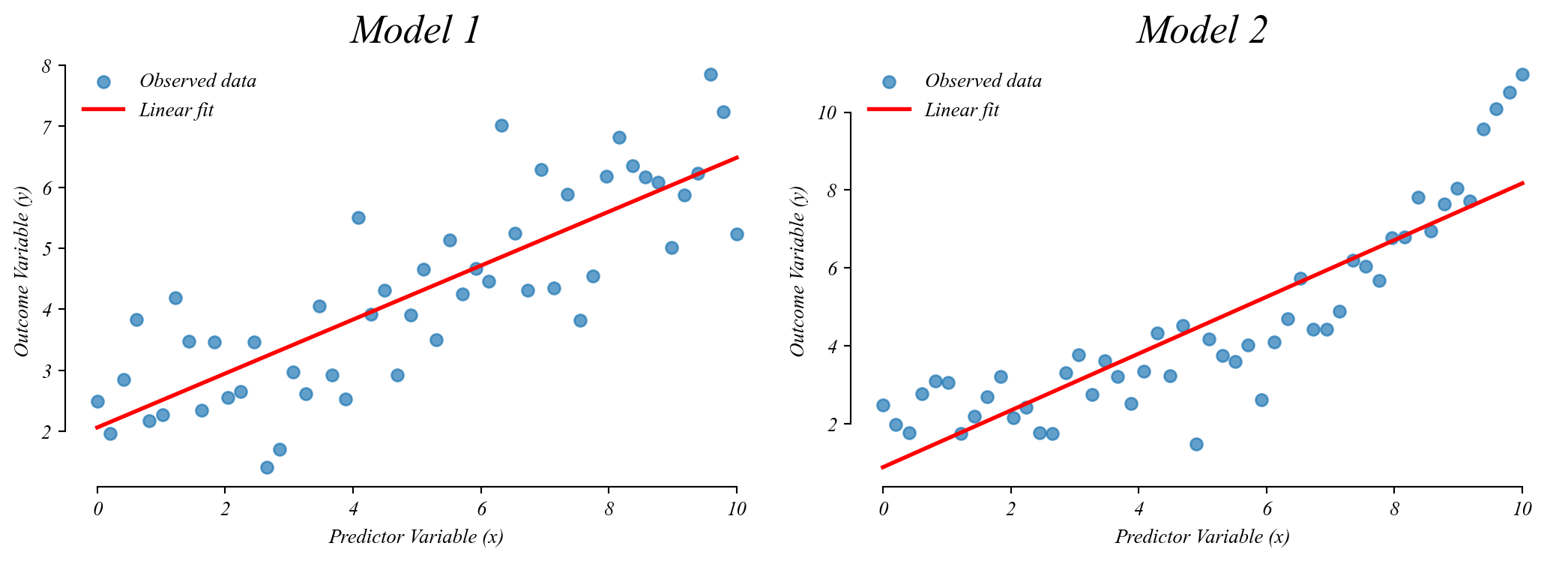
> our model will offer inaccurate predictions if some assumptions aren’t met

GLM Assumptions

Our test results are only valid when the model assumptions are valid.


  1. Linearity: The relationship between X and Y is linear
  1. Homoskedasticity: Equal error variance across all values of X
  1. Normality: Errors are normally distributed
  1. Independence: Observations are independent from each other

GLM Assumptions: why check?

Assumption violations affect our inferences


If assumptions are violated:

  • Coefficient estimates may be biased
  • Standard errors may be wrong
  • p-values may be misleading
  • Predictions may be unreliable

> to test whether the model is ‘specified’, we can calculate the residuals and the model predictions

Model Residuals

… we can directly examine the error of the model. 


# Calculate residuals
residuals = model.resid
sns.histplot(residuals)

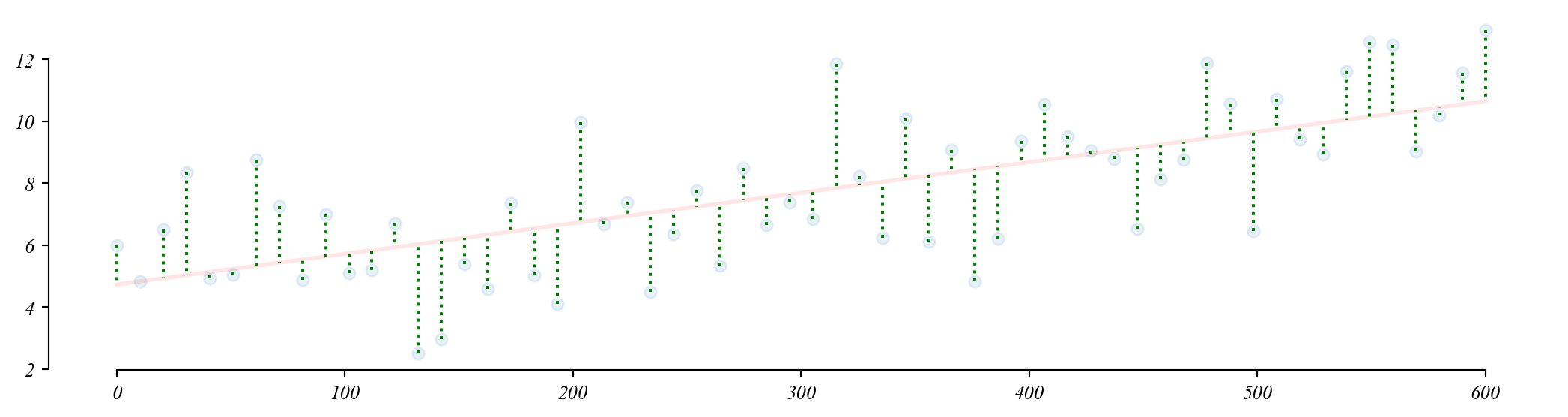
> this is \(\varepsilon\)

Model Predictions

… we can directly examine the predictions of the model. 


# Calculate predictions
predictions = model.predict()
sns.histplot(predictions)

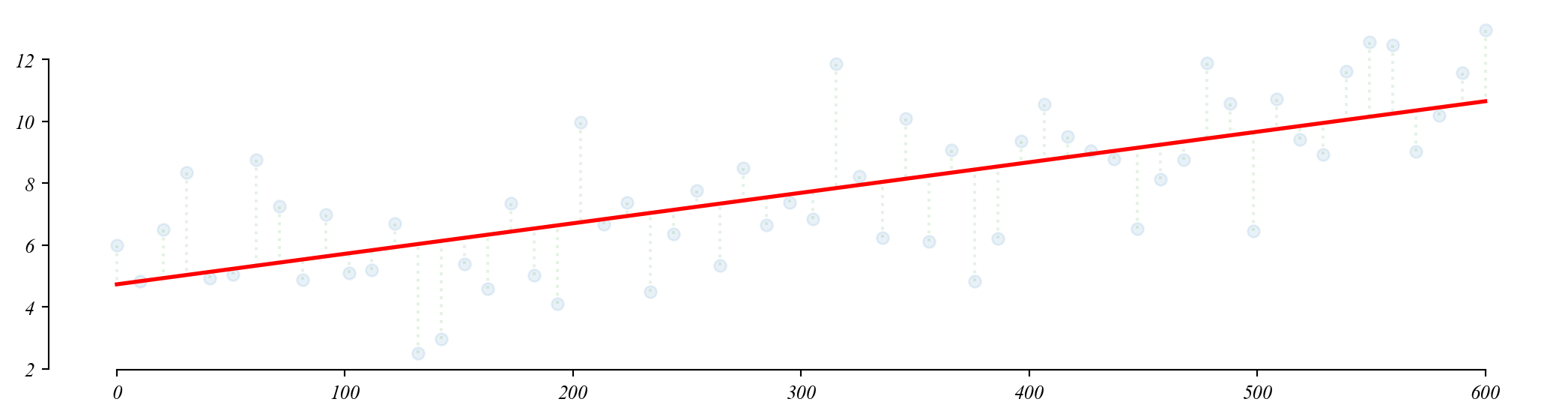
> this is \(\hat{y}\), the model prediction

Exercise 4.2 | Residual Plot of Happiness and GDP

A Residual Plot directly visualizes the error for each model estimate. 



# Residual Plot: predictions against residuals
plt.scatter(predictions, residuals)

Assumption 1: Checking for Linearity

The error term should be unrelated to the fitted value.

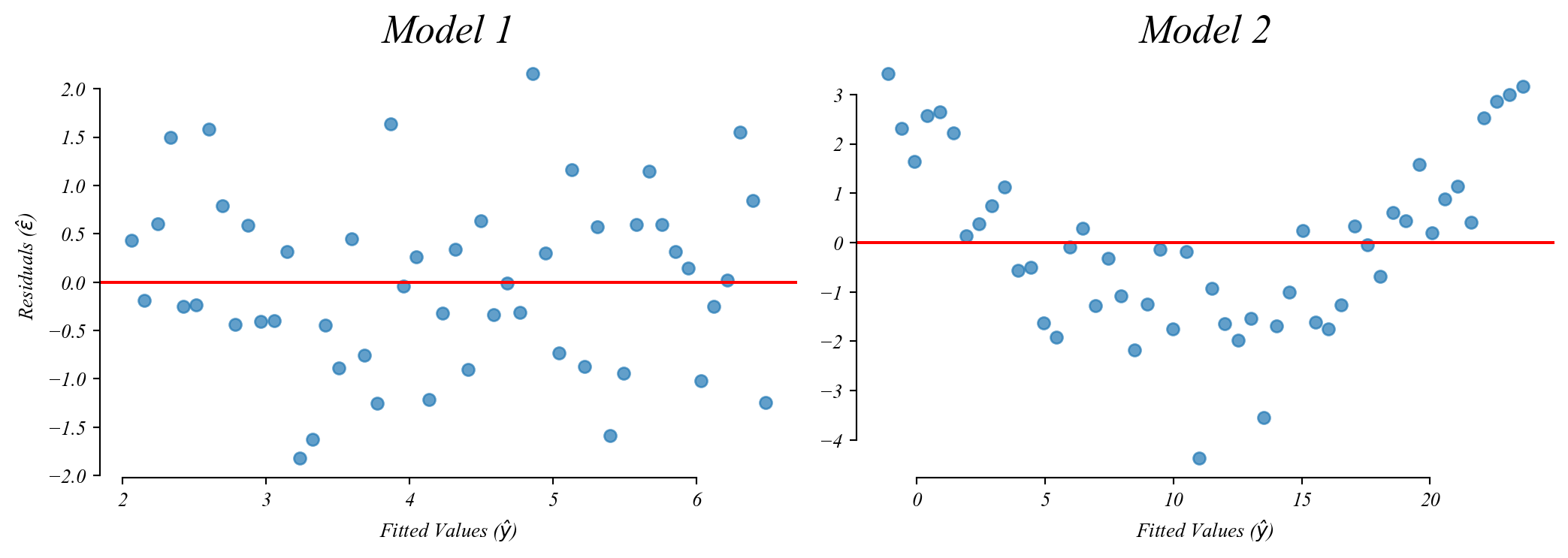
> the left figure shows that the model is equally wrong everywhere

> the right figure shows that the model is a good fit at only some values

Assumption 1: Checking for Linearity

A non-linear relationship will produce non-linear residuals.

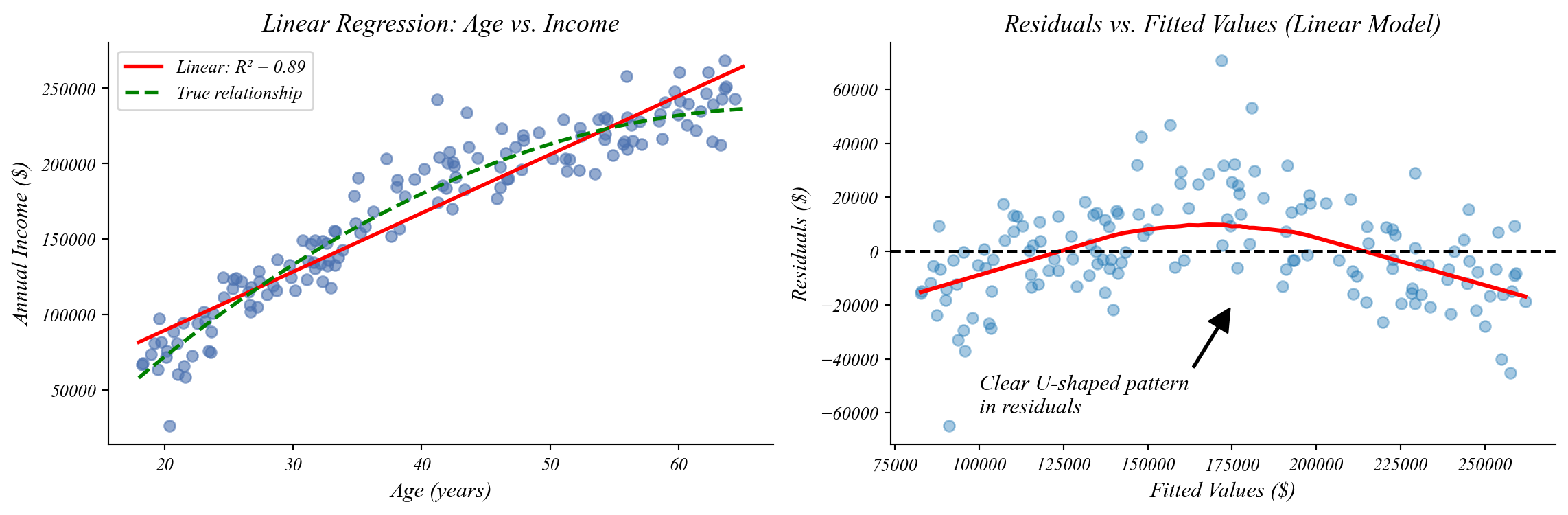
> linear model misses curvature, leading to systematic errors

Handling Non-Linear Relationships

Transform variables to become linear

Adding a square term or performing a log transformation can fix the problem.


instead of

\[\text{income} = \beta_0 + \beta_1 \text{age} + \varepsilon\]

we could use

\[\text{income} = \beta_0 + \beta_1 \text{age} + \beta_2 \text{age}^2 + \varepsilon\]

It’s also common to log transform either the \(x\) or \(y\) variable.

Assumption 2: Homoskedasticity

Residuals should be spread out the same everywhere.

Which one of these figures shows homoskedasticity?

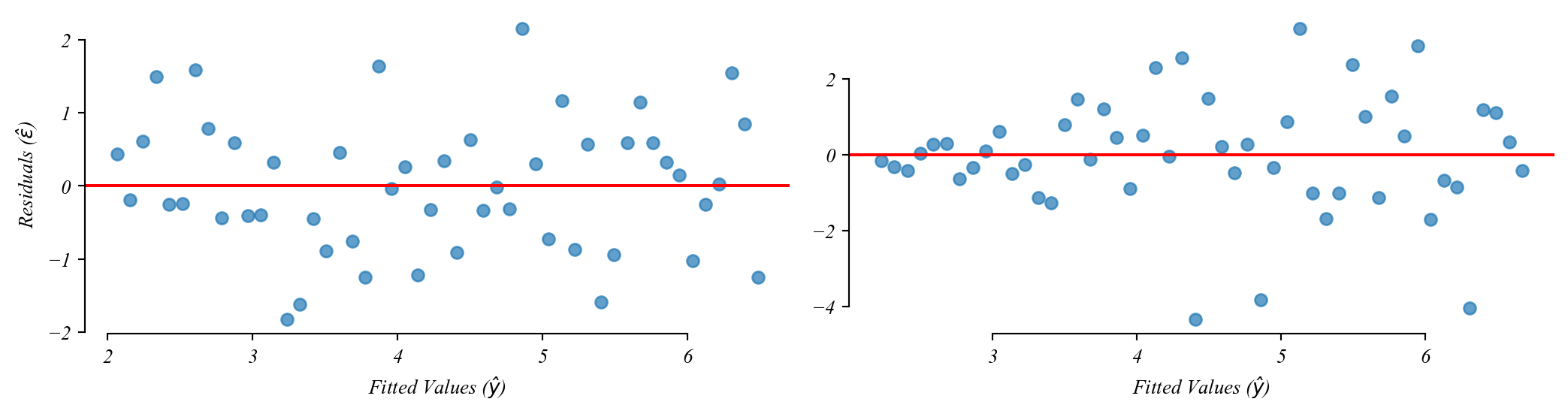
> the left figure shows constant variability (homoskedasticity)

> the right figure shows increasing variability (heteroskedasticity)

> residual plots should show that the model is equally wrong everywhere

Assumption 2: Homoskedasticity

The spread of residuals should not change across values of X.

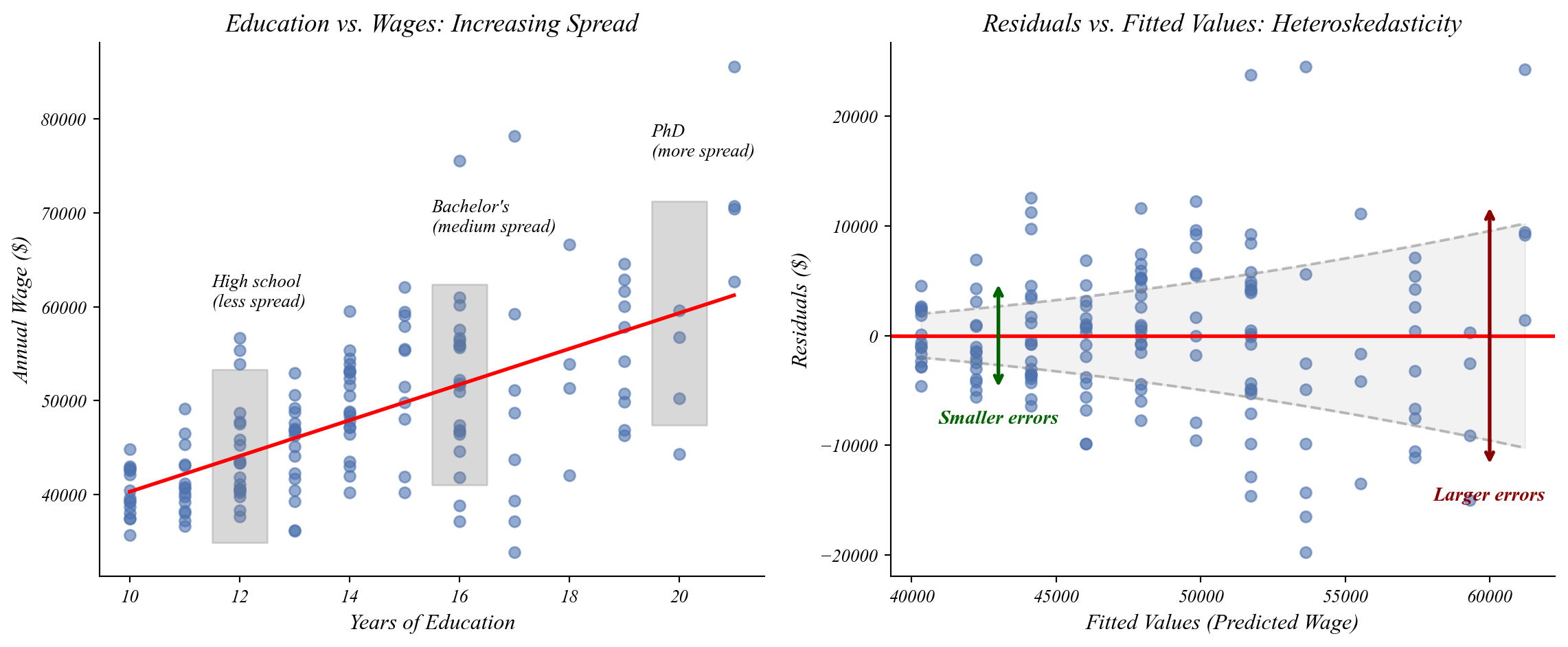
> the spread of points increases as education increases

> PhD wages vary more than high school wages

Handling Heteroskedasticity

Robust standard errors give more accurate measures of uncertainty



Robust Standard Errors adjust for the changing spread in our data.

Use robust standard errors to give more accurate hypothesis tests.



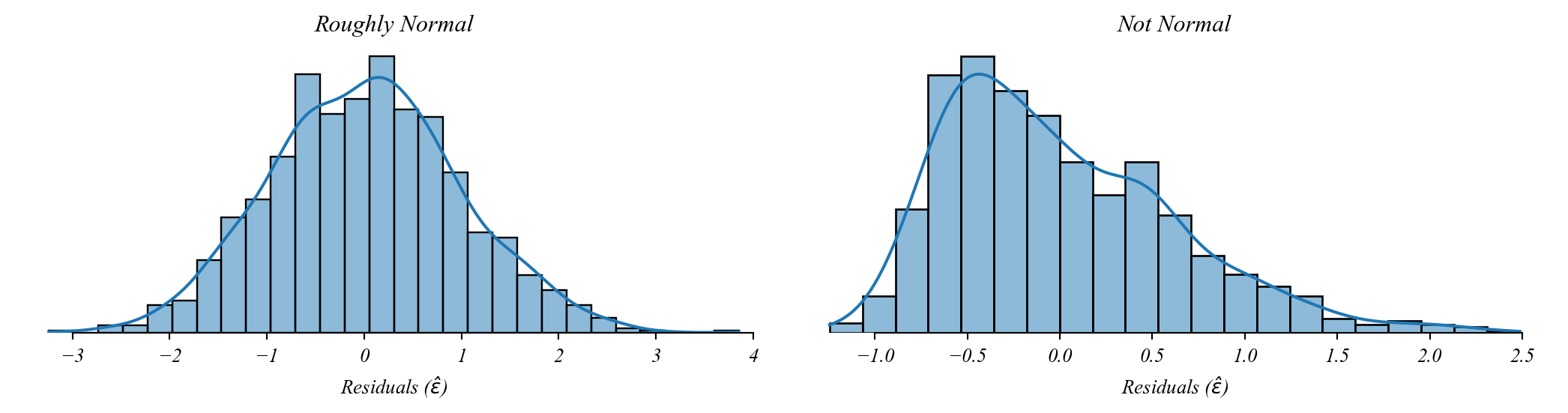
# Fit the model with robust standard errors (HC3: heteroskedastic-constant)
robust_model = smf.ols('wages ~ education', data=df).fit(cov_type='HC3')

Assumption 3: Normality

Residuals should be normally distributed.

By the CLT we can still use GLM without this so long as the sample is large.

Assumption 4: Indepedence

Observations are independent from each other



We’ll return to this assumption in Part 4.4 | Timeseries.

Looking Forward

Extending the GLM framework

Next Up:

  • Part 4.3 | Categorical Predictors
  • Part 4.4 | Timeseries
  • Part 4.5 | Causality

Later:

  • Part 5.1 | Numerical Controls
  • Part 5.2 | Categorical Controls
  • Part 5.3 | Interactions
  • Part 5.4 | Model Selection

> all built on the same statistical foundation