ECON 0150 | Economic Data Analysis

The economist’s data analysis stillset.


Part 4.1 | Numerical Predictors

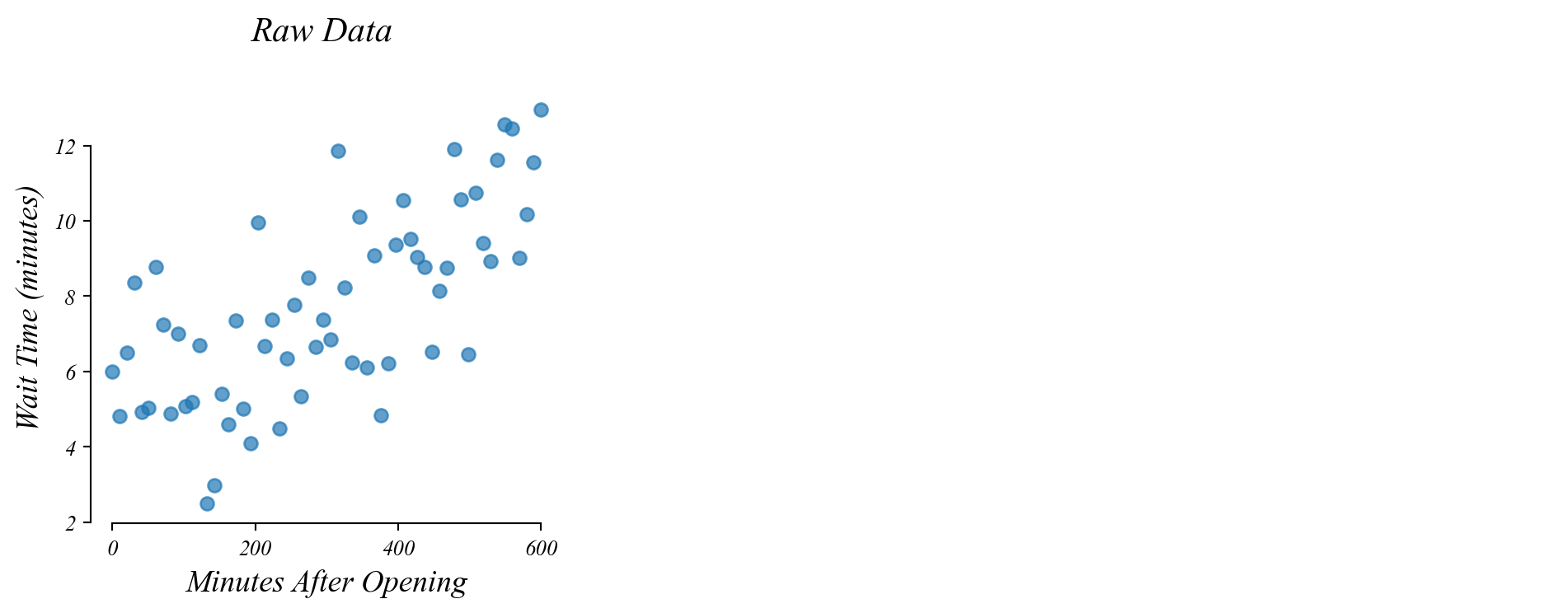
GLM: bivariate data

Do people wait longer later in the day?

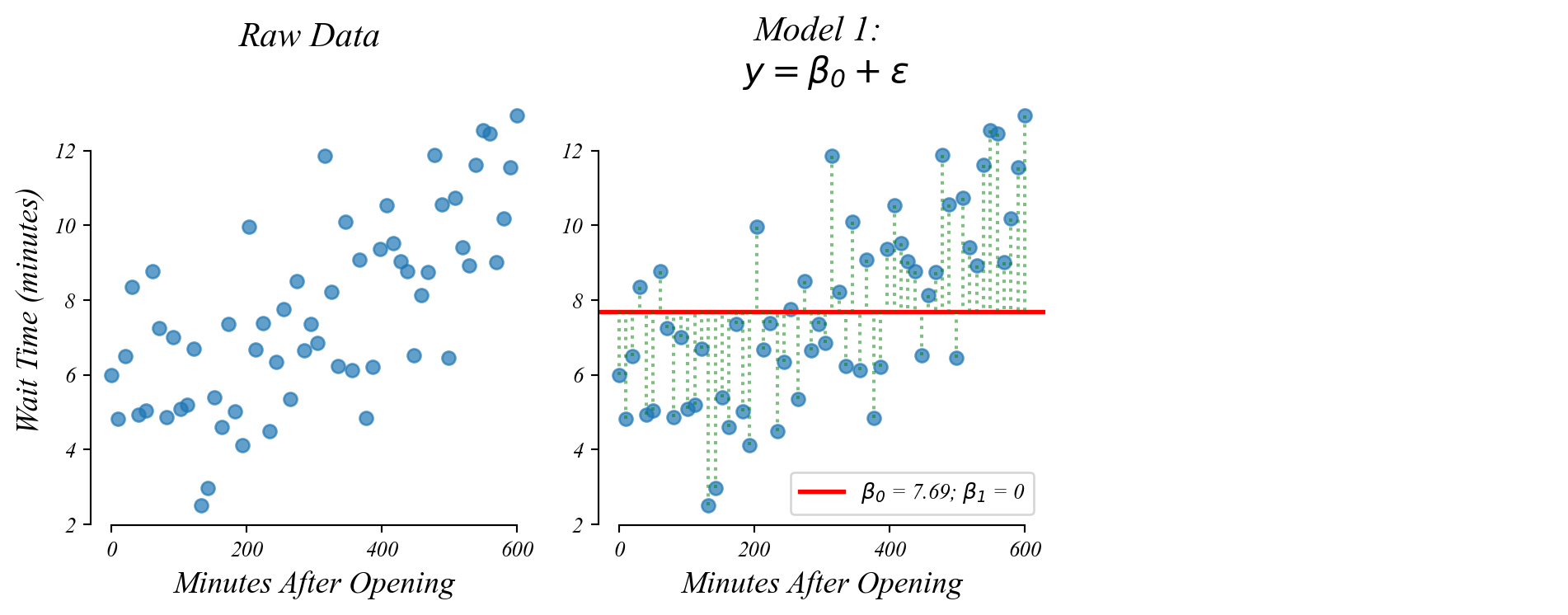
GLM: bivariate data

Do people wait longer later in the day?

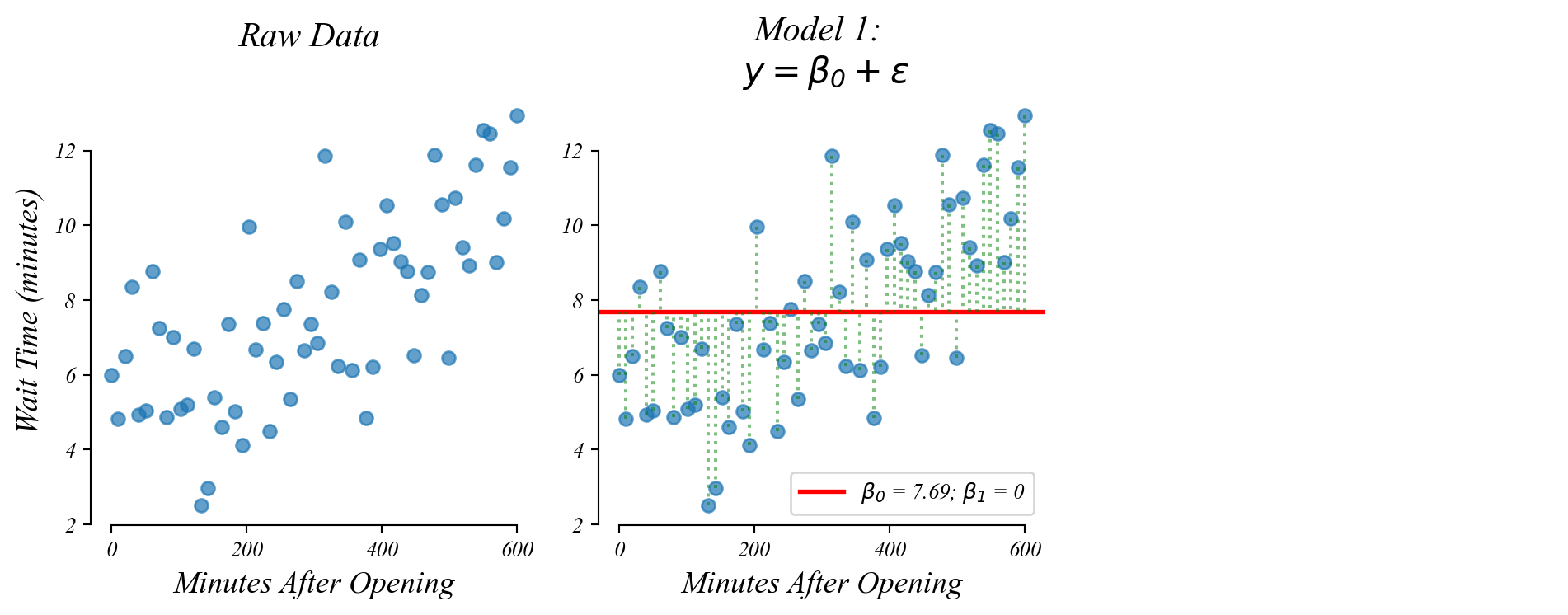
> but in general we don’t ask many questions about vertical incercepts

GLM: bivariate data

Do people wait longer later in the day?

Lets compare two models.

  • Model 1 (Intercept Only): \(y = b\)
  • Model 2 (Intercept+Slope): \(y = mx + b\)

GLM: bivariate data

Do people wait longer later in the day?

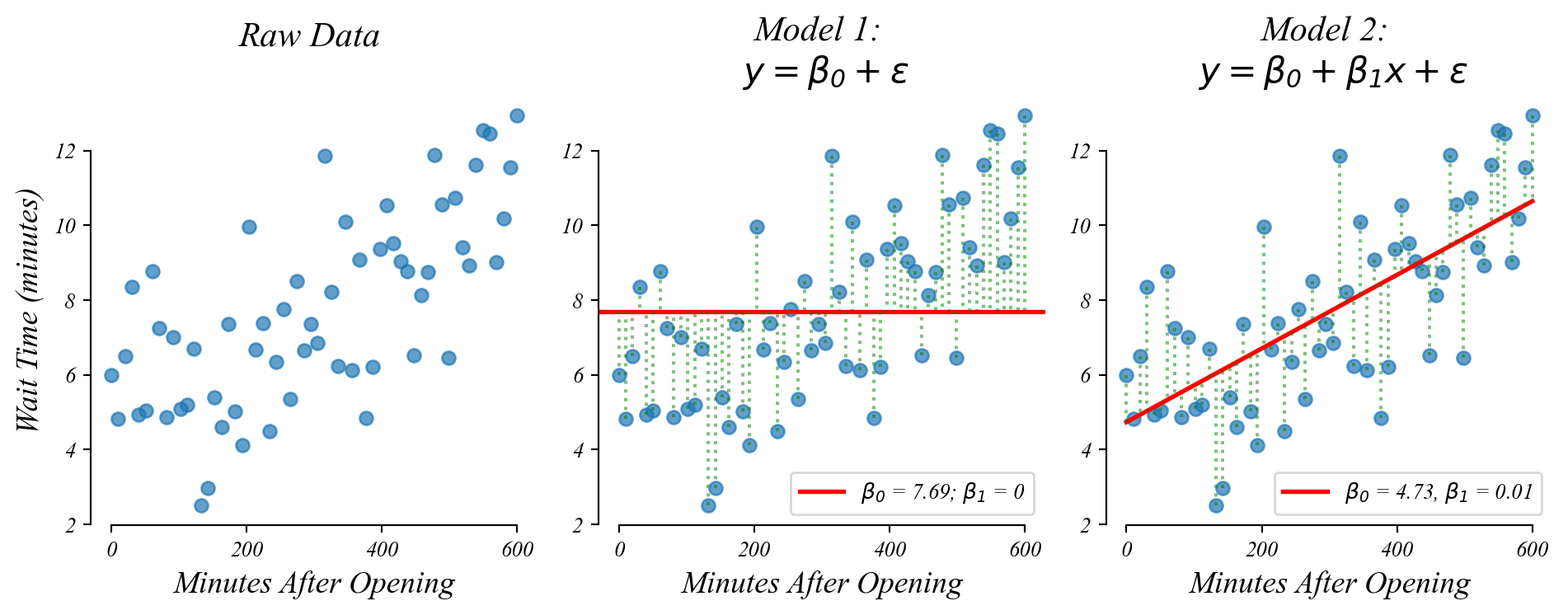
> a slope (β₁) improves model fit (MSE; ‘wrongness’) when there’s a relationship

> the intercept is no longer the mean

Bivariate GLM: minimizing MSE

Which model minimizes the models’ ‘wrongness’ (Mean Squared Error)?

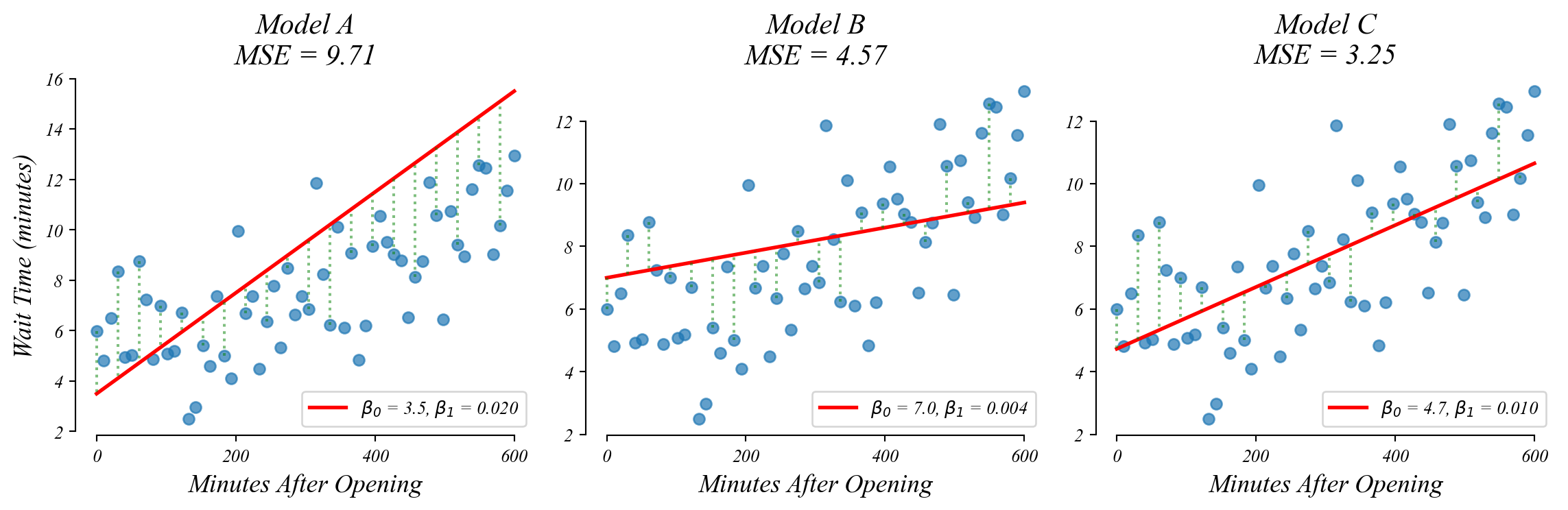
> Model C minimizes MSE!

Bivariate GLM: minimizing MSE

GLM selects the \(\beta_1\) with the smallest MSE.

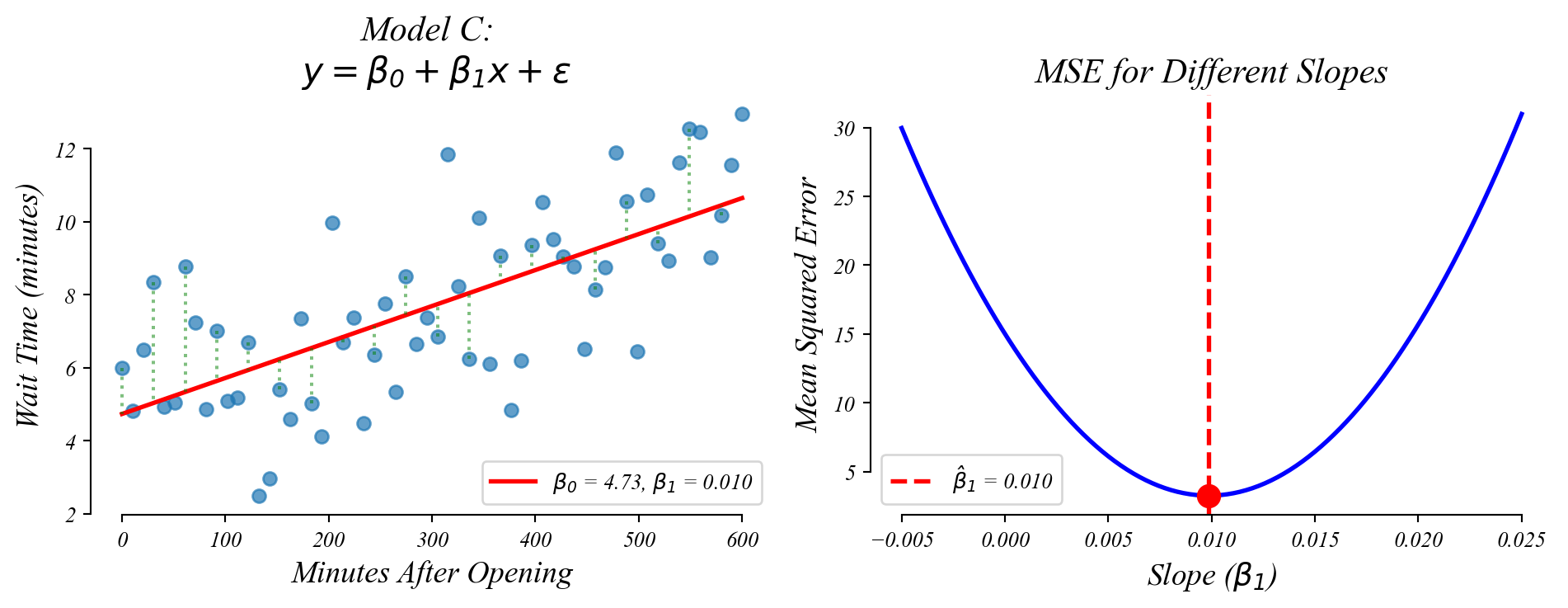
> this slope (β₁) gives the best guess of the relationship between x and y

> but what if the true slope is zero … could this slope be just sampling error?

Bivariate GLM: sampling error

Like before, if we take many samples, we get slighly different slopes and slighly different fits.

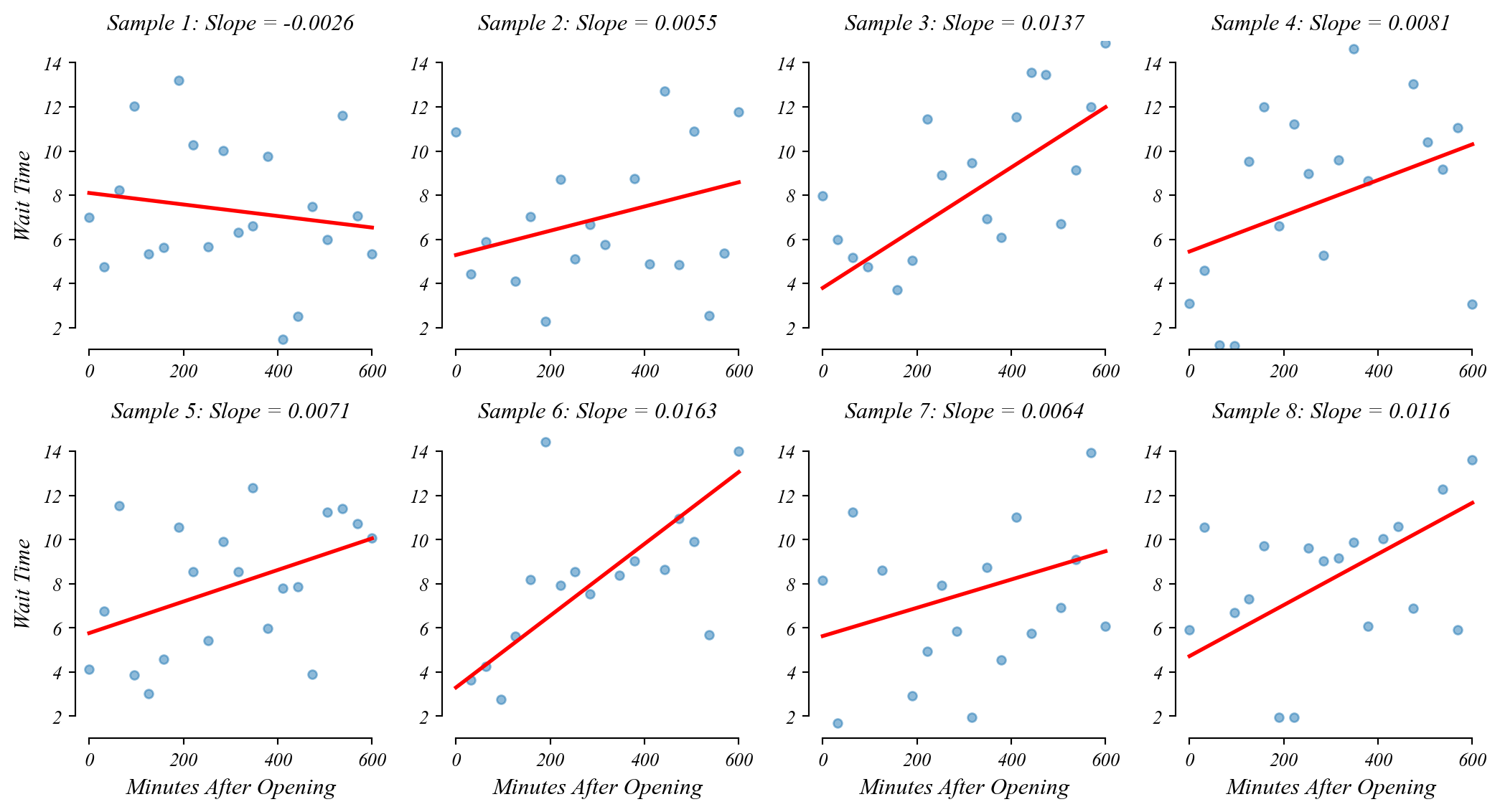
Bivariate GLM: sampling distribution of slopes

The slope coefficient follows a normal distribution centered on the population slope.

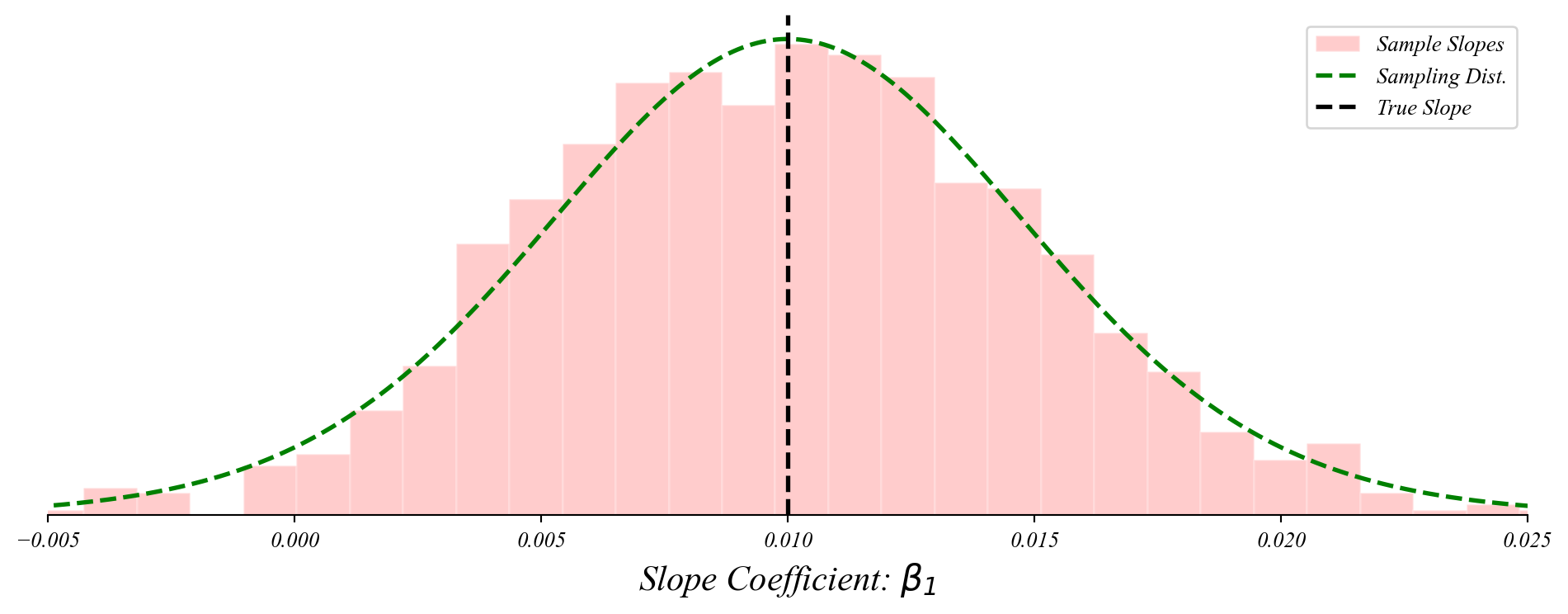
> the slopes follow a normal distribution around the population relationship!

> this lets us perform a t-test on the slope!

Bivariate GLM: sampling distribution of slopes

The slope coefficient follows a normal distribution centered on the population slope.

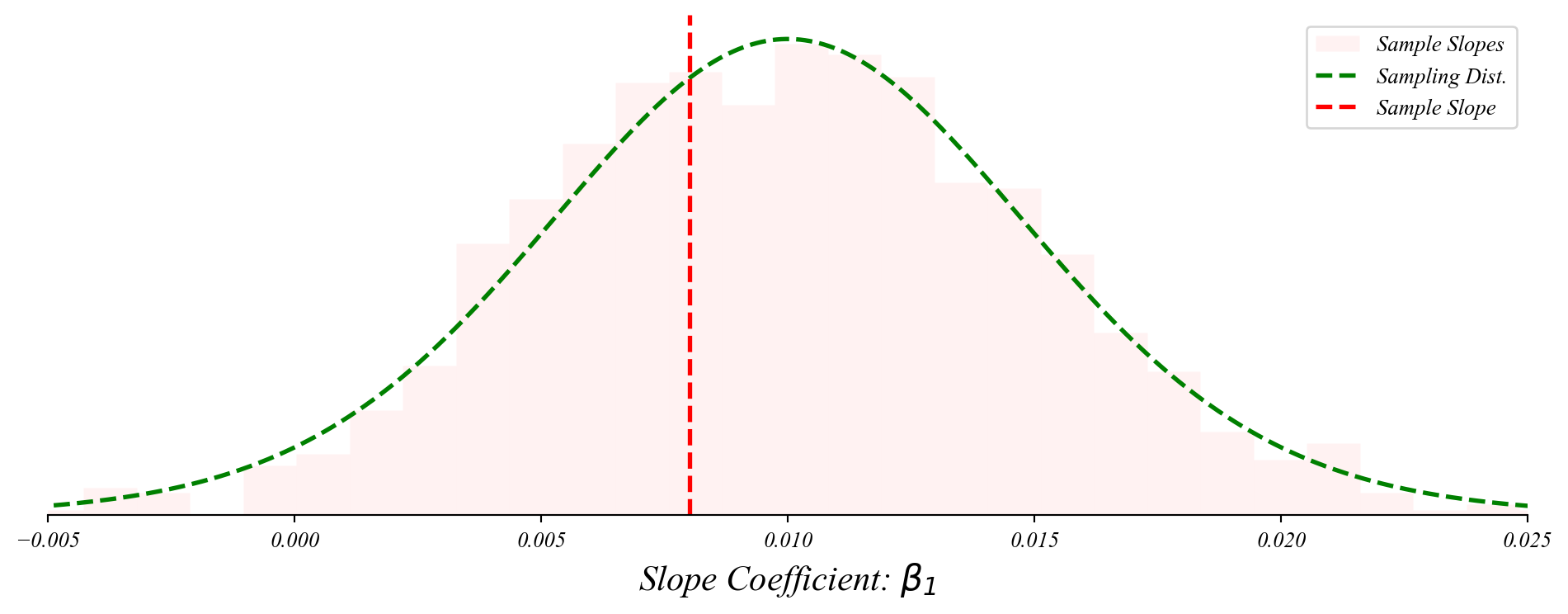
> we don’t know the entire distribution, just our sample slope

Bivariate GLM: sampling distribution of slopes

The slope coefficient follows a normal distribution centered on the population slope.

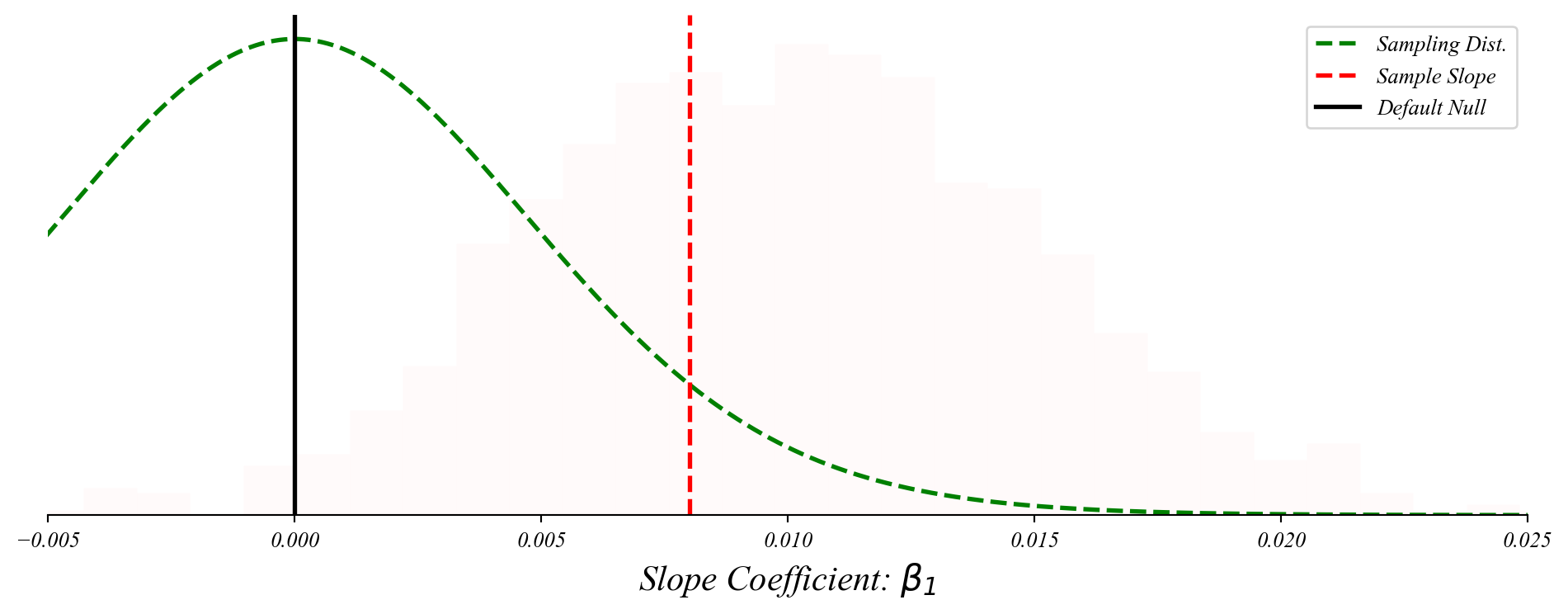
> center the distribution on our null

> check the distance from the sample

Bivariate GLM: sampling distribution of slopes

The slope coefficient follows a normal distribution centered on the population slope.

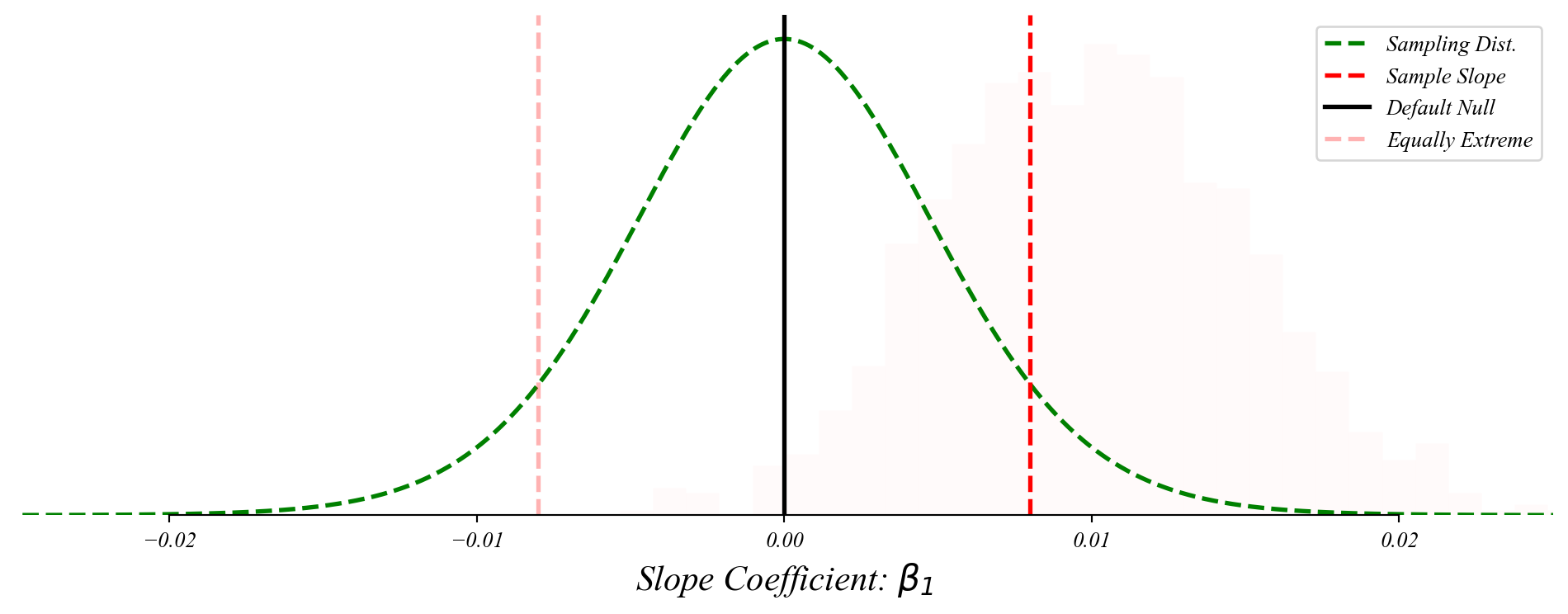
> the p-value is the probability of something as far from the null as our sample

Bivariate GLM: sampling distribution of slopes

The slope coefficient follows a normal distribution centered on the population slope.

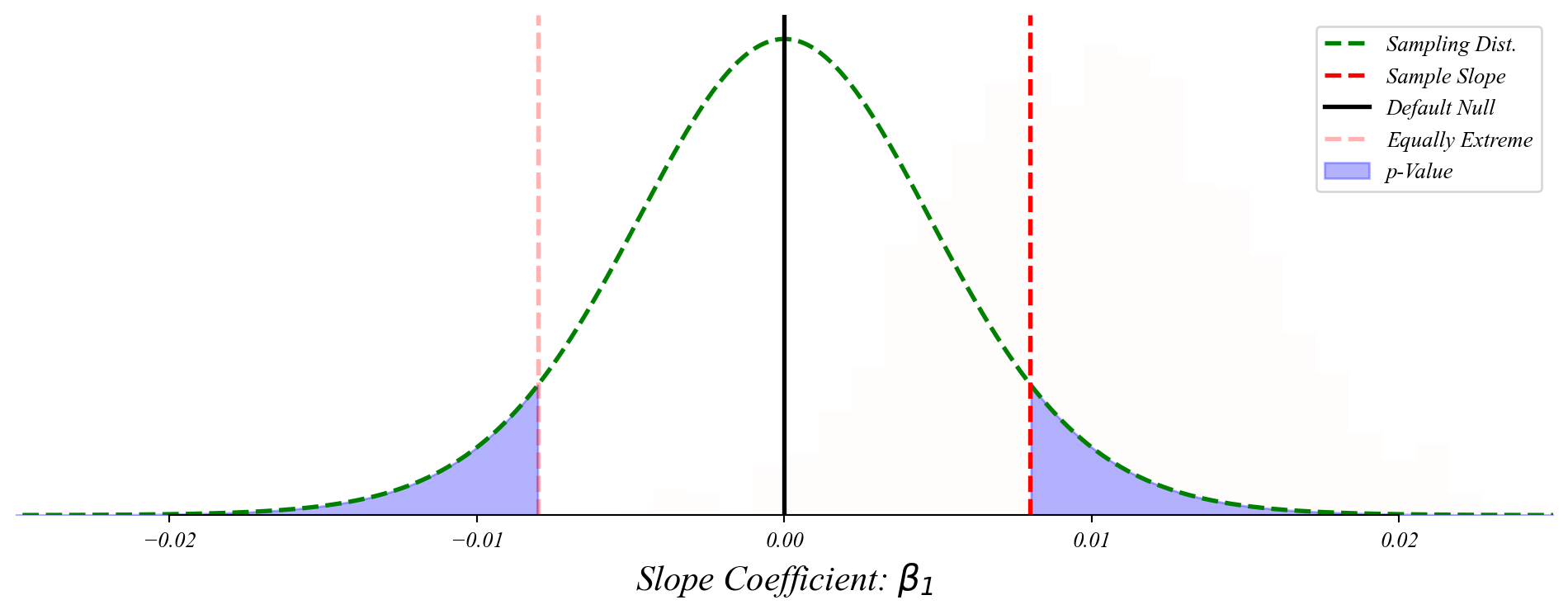
> p-value: the ‘surprisingness’ of our sample if \(\beta_1 = 0\)

> the probability of seeing our sample by chance if there is no relationship

> a small p-value is evidence against the null hypothesis (\(\beta_1 = 0\))

Bivariate GLM: sampling distribution of slopes

Many possible models we might observe by chance if the null (\(\beta_1 = 0\)) were true.

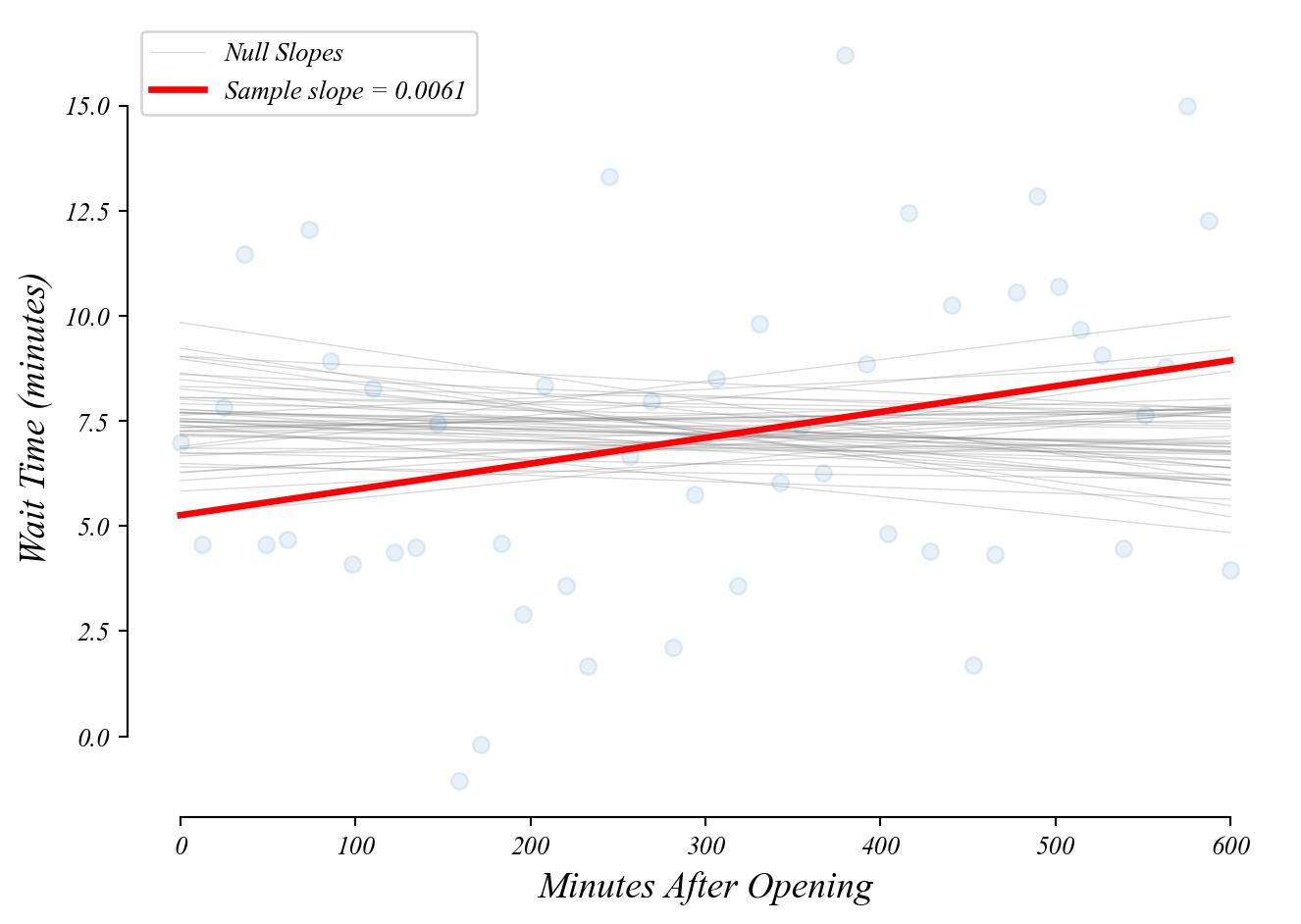
> how likely does it look like this slope was drawn from the null slopes?

> p-value: the probability a slope as extreme as ours under the null (\(\beta_1=0\))

Exercise 4.1 | Happiness and Per Capita GDP

Are wealtheir countries happier? 



# Model: y = b + mx
model = smf.ols('Life_Evaluation ~ log_GDP_PerCap', data).fit() # Intercept is included by default
print(model.summary().tables[1])


# Visualize: Numerical x Numerical
sns.regplot(data=data, y='Life_Evaluation', x='log_GDP_PerCap')#, ci=None), line_kws={'color': 'red'}

GLM: predictions

What wait time should we expect at 100 minutes after open?

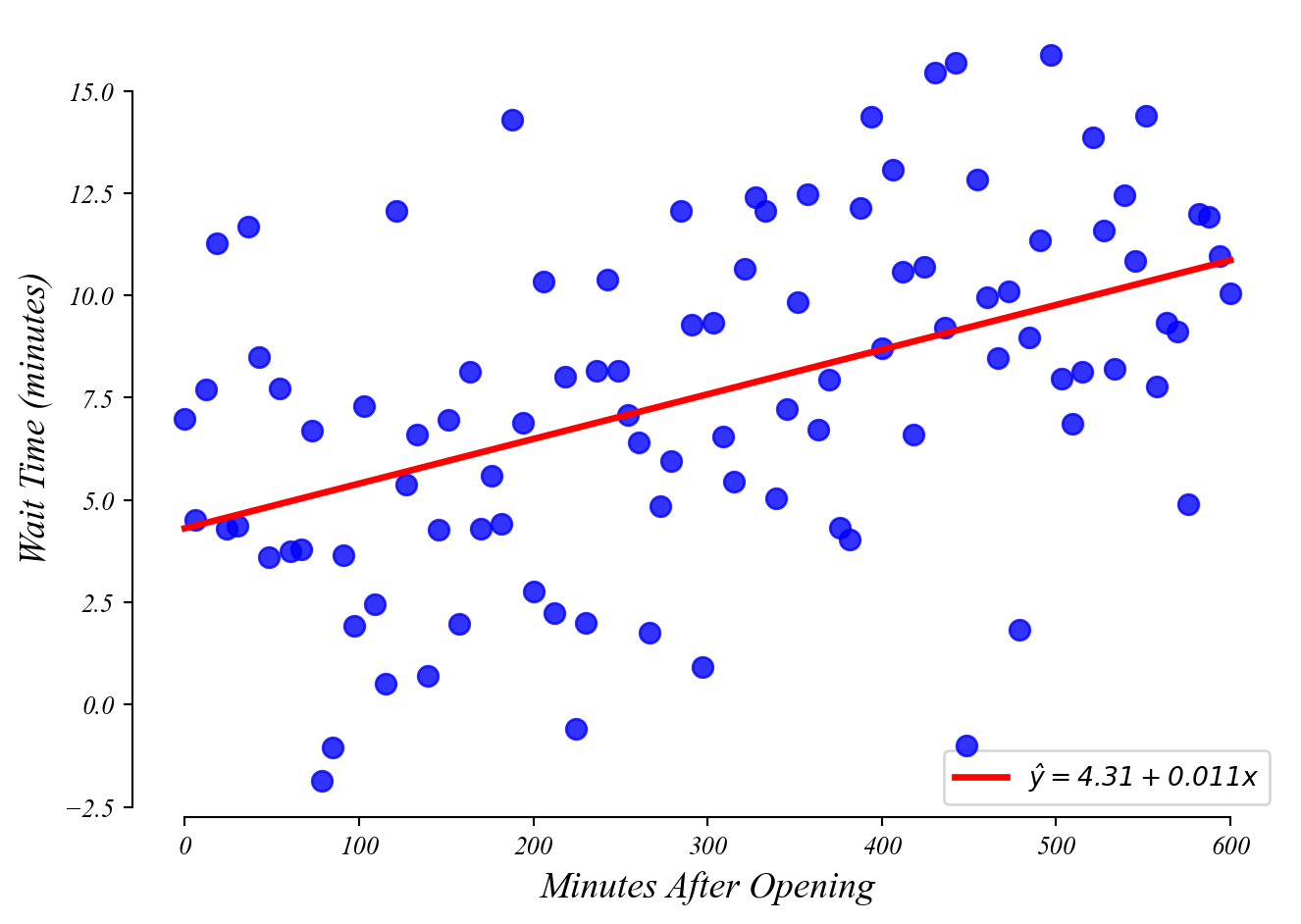
GLM: predictions

What wait time should we expect at 100 minutes after open?

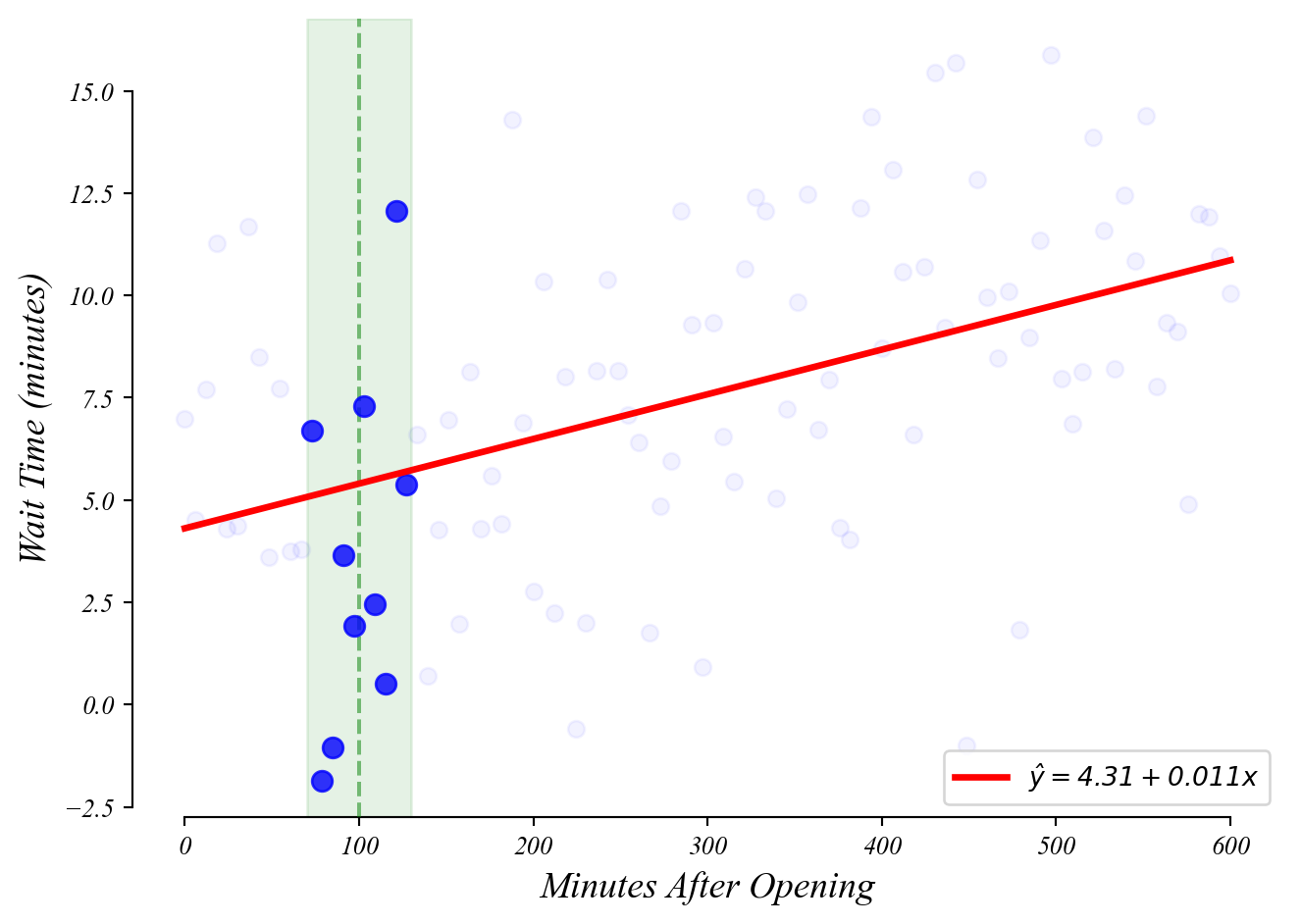
GLM: predictions

What wait time should we expect at 100 minutes after open?

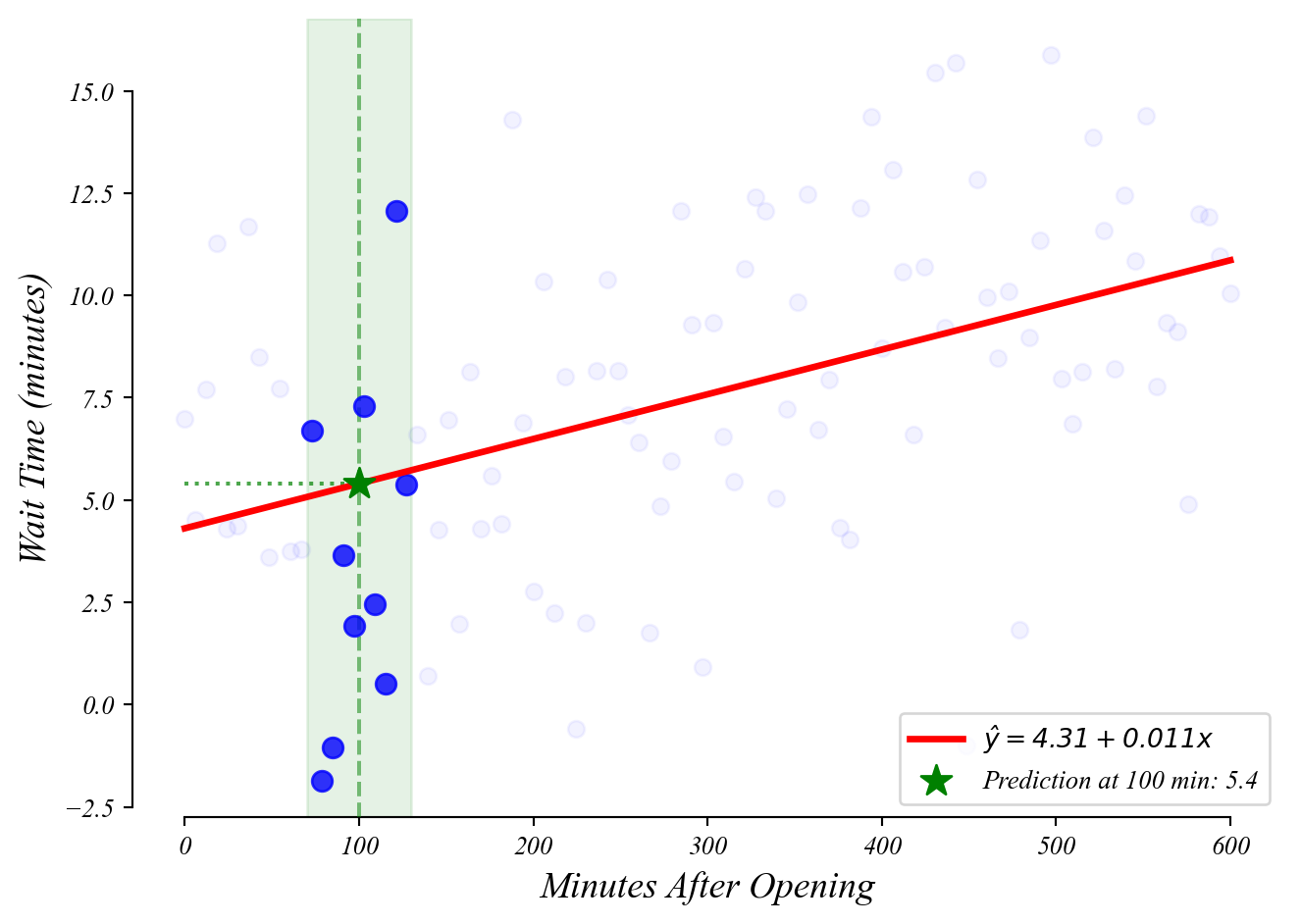
> you can find this with a calculator!

> plug \(x=100\) into the equation \(y = 4.31 + 0.011 x\)

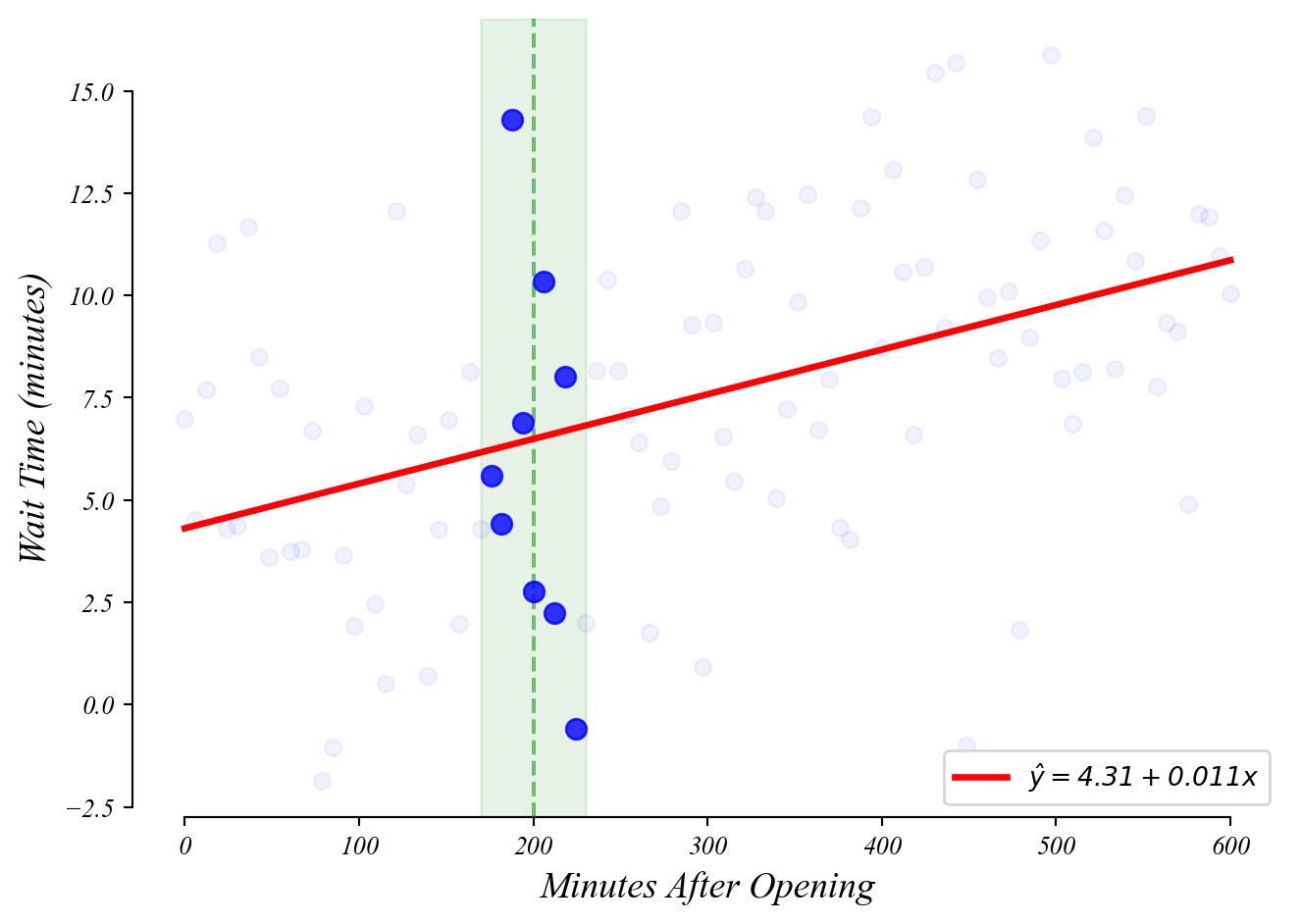
GLM: predictions

What wait time should we expect at 200 minutes after open?

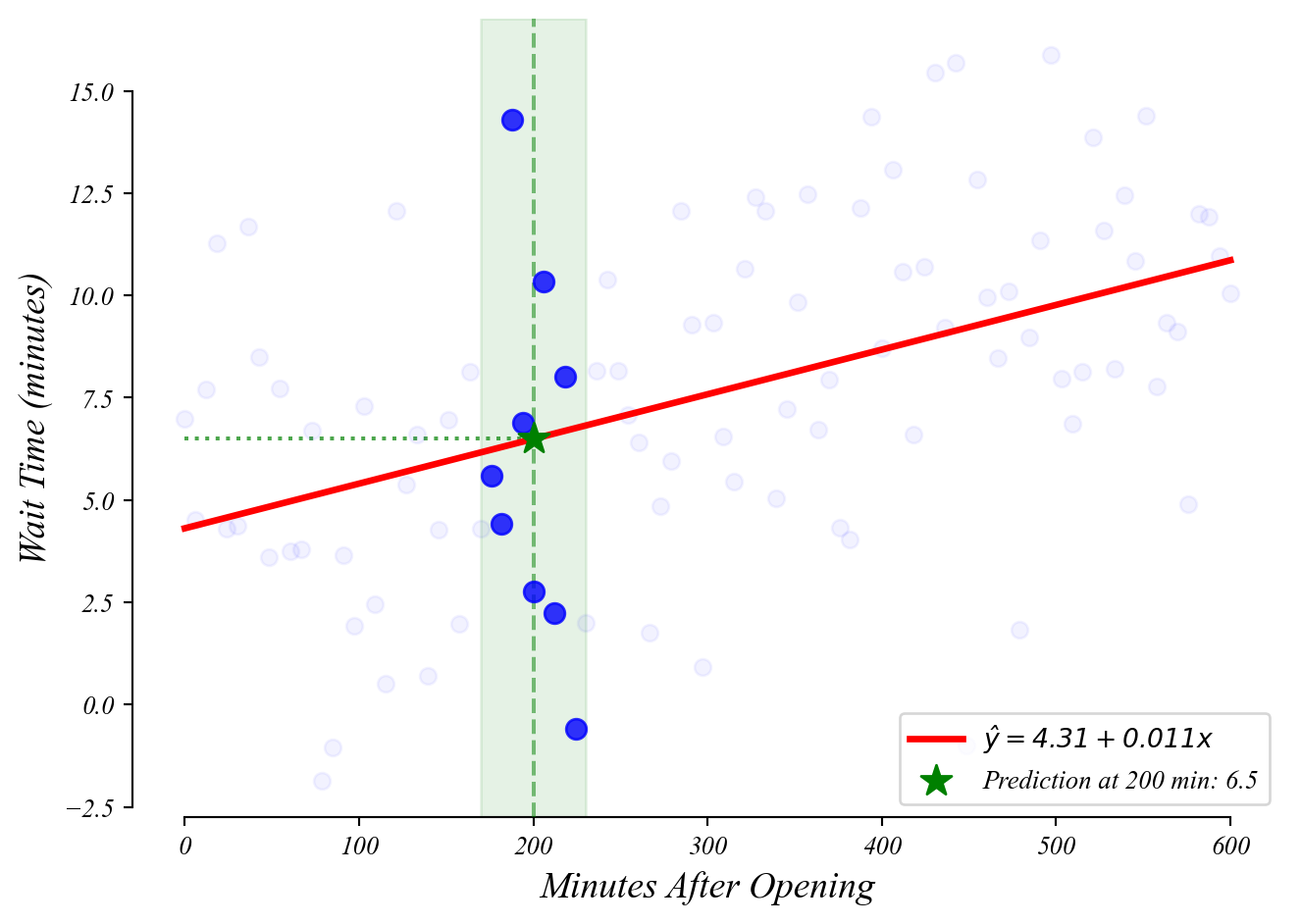
GLM: predictions

What wait time should we expect at 200 minutes after open?

Exercise 4.1 | Happiness and Per Capita GDP

Are wealtheir countries happier? 



# Parameters
b0, b1 = model.params  # intercept, slope


# Predict: Log GDP of 3
prediction = b0 + b1 * 3
print(prediction)

GLM: interpretation

How much does wait time increase every minute after open?

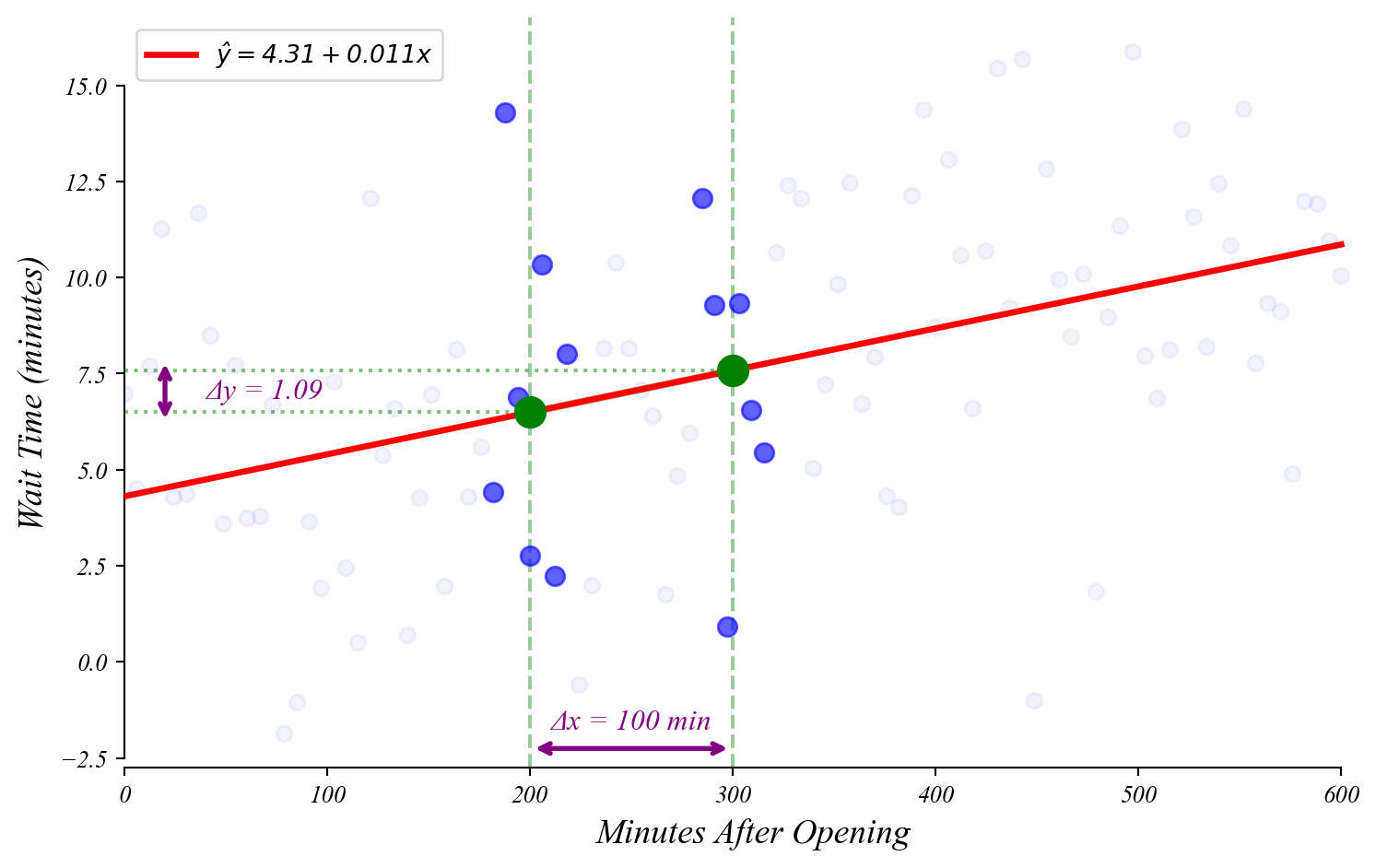
> \(\beta_1\) tells us how much \(y\) increases with every 1 unit increase in \(x\)

Exercise 4.1 | Happiness and Per Capita GDP

How much does happiness increase for each additional $1,000 of per capita GDP?

The General Linear Model

GLM performs a t-test on all model coefficients.

Univariate (Part 3): \(y = \beta_0 + \epsilon\)

  • Equivalent to a one-sample t-test
  • Tests whether \(\beta_0 = \mu_0\) (default null)

Numerical Predictor: \(y = \beta_0 + \beta_1 x + \epsilon\)

  • \(x\) is a numerical variable (like age, income, temperature, etc.)
  • Tests both intercept (\(\beta_0 = 0\)) and slope (\(\beta_1 = 0\))
  • Null hypothesis on slope: no relationship between x and y (\(\beta_1 = 0\))

The General Linear Model

GLM uses the idea of a t-test with any coefficient.

Categorical Predictor (next time): \(y = \beta_0 + \beta_1 x + \epsilon\)

  • \(x\) is a categorical variable (like age, income, temperature, etc.)
  • Equivalent to a two-sample t-test (when \(x\) is binary)

Multivariate GLM (Part 5):

  • Adds more predictor variables: \(y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + ... + \varepsilon\)
  • Each coefficient has its own t-test against the null that it equals zero

Economic Applications

GLM is the workhorse statistical tool in empirical economics.

Labor Economics: relationship between education and wages.

\[\text{wage} = \beta_0 + \beta_1 \text{education} + \varepsilon\]

Policy Analysis: relationship between minimum wages and employment.

\[\text{employment} = \beta_0 + \beta_1 \text{minimum_wage} + \varepsilon\]

Political Economy: relationship between neighbor’s party and voter turnout

\[\text{voted} = \beta_0 + \beta_1 \text{neighborhood_politics} + \varepsilon\]

Bivariate GLM: Numerical Predictors

Summary

GLM Framework:

  • T-tests and regression are part of the same very flexible framework.

Numerical Predictors:

  • Bivariate GLM extends the t-test by allowing continuous predictors.

Same Distribution:

  • Coefficient estimates follow t-distributions centered on the true population values.

Same Interpretation:

  • The p-values have the same interpretation: probability of seeing results this extreme if the null is true.

Looking Forward

Extending the GLM framework

Next Up:

  • Part 4.2 | Bad Models
  • Part 4.3 | Categorical Predictors
  • Part 4.4 | Timeseries
  • Part 4.5 | Causality

Later:

  • Part 5.1 | Numerical Controls
  • Part 5.2 | Categorical Controls
  • Part 5.3 | Interactions
  • Part 5.4 | Model Selection

> all built on the same statistical foundation