ECON 0150 | Economic Data Analysis

The economist’s data analysis stillset.

Part 3.5 | The Simplest Linear Model

General Linear Model (GLM)

The General Linear Model just draws lines through data points.

We just developed the simplest GLM!

General Linear Model (GLM)

The General Linear Model just draws lines through data points.

What is a GLM?

• Basically just a line drawn through the data.

Linear Model Equation: \(y = mx + b\)

• We call \(y\) the ‘outcome variable’ (numerical only in this class)

• We call \(x\) the ‘predictor variable’ (categorical or numerical)

• Can have more than one predictor variable: \(y = m_1 x_1 + m_2 x_2 + b\)

• If you want to be fancy, write it like: \(y_i = mx_i + b + \epsilon_i\)

General Linear Model (GLM)

The General Linear Model just draws lines through data points.

How do we choose the line?

• We minimize the ‘wrongness’ of the model.

Mean Sqaured Error: \(MSE = \frac{1}{n} \sum_i \epsilon_i^2\)

• This \(\epsilon_i\) is just how wrong our model is for data point \(i\)

• This is just the average distance between the line and a data point.

• This is very similar to Variance!

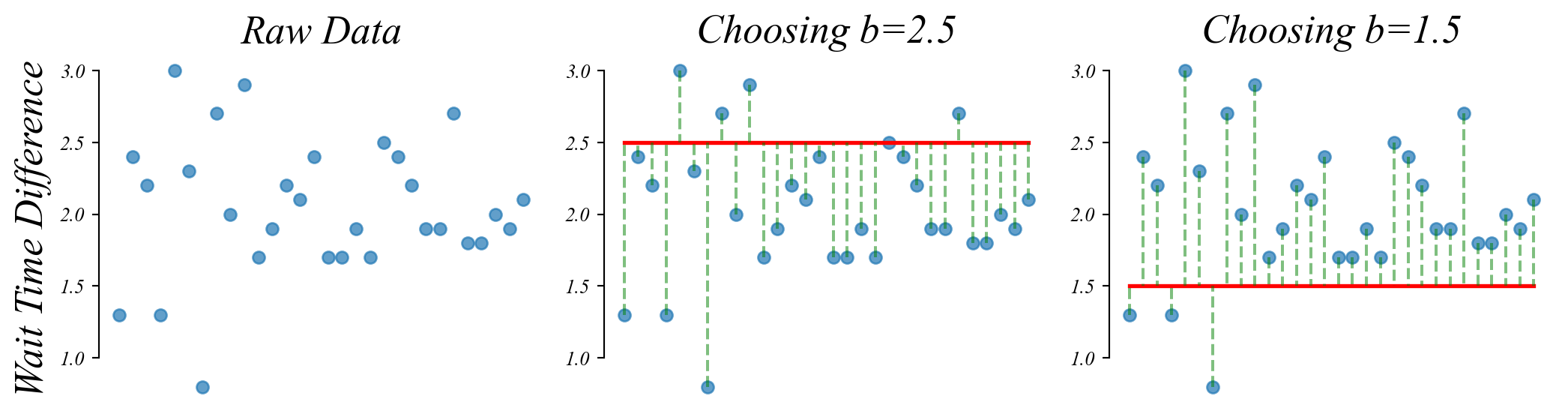
GLM: Intercept-Only

A model with no x ( basically: x=0 ).

The simplest GLM is using only an intercept term: \(y=b\).

• The data \(x_i\) is in blue.
• The model \(b\) is in red.
• The error \(\epsilon_i\) is in green.

> what should we choose for b to minimize the model’s error?

GLM: Line Fitting and the Sample Mean

The sample mean minimizes the MSE.

We minimize the MSE by choosing \(b\) to be equal to the sample mean \(\bar{y}\).

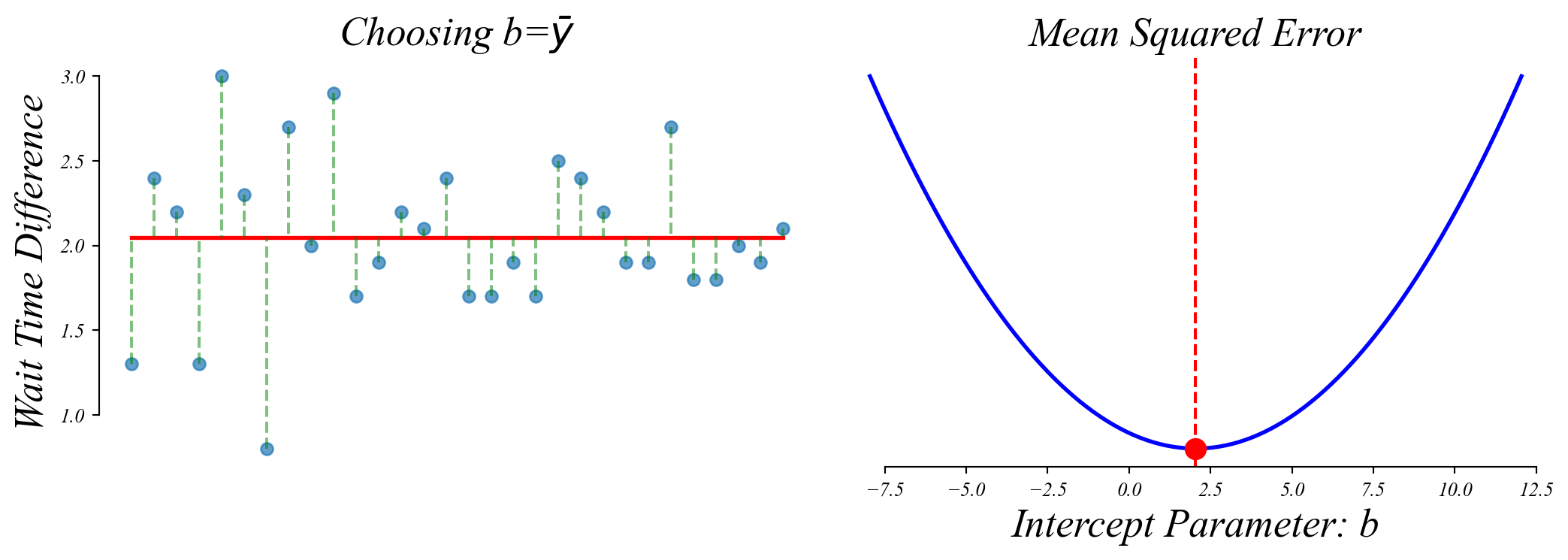
> when we’ve minimized MSE, it’s equal to the Variance!

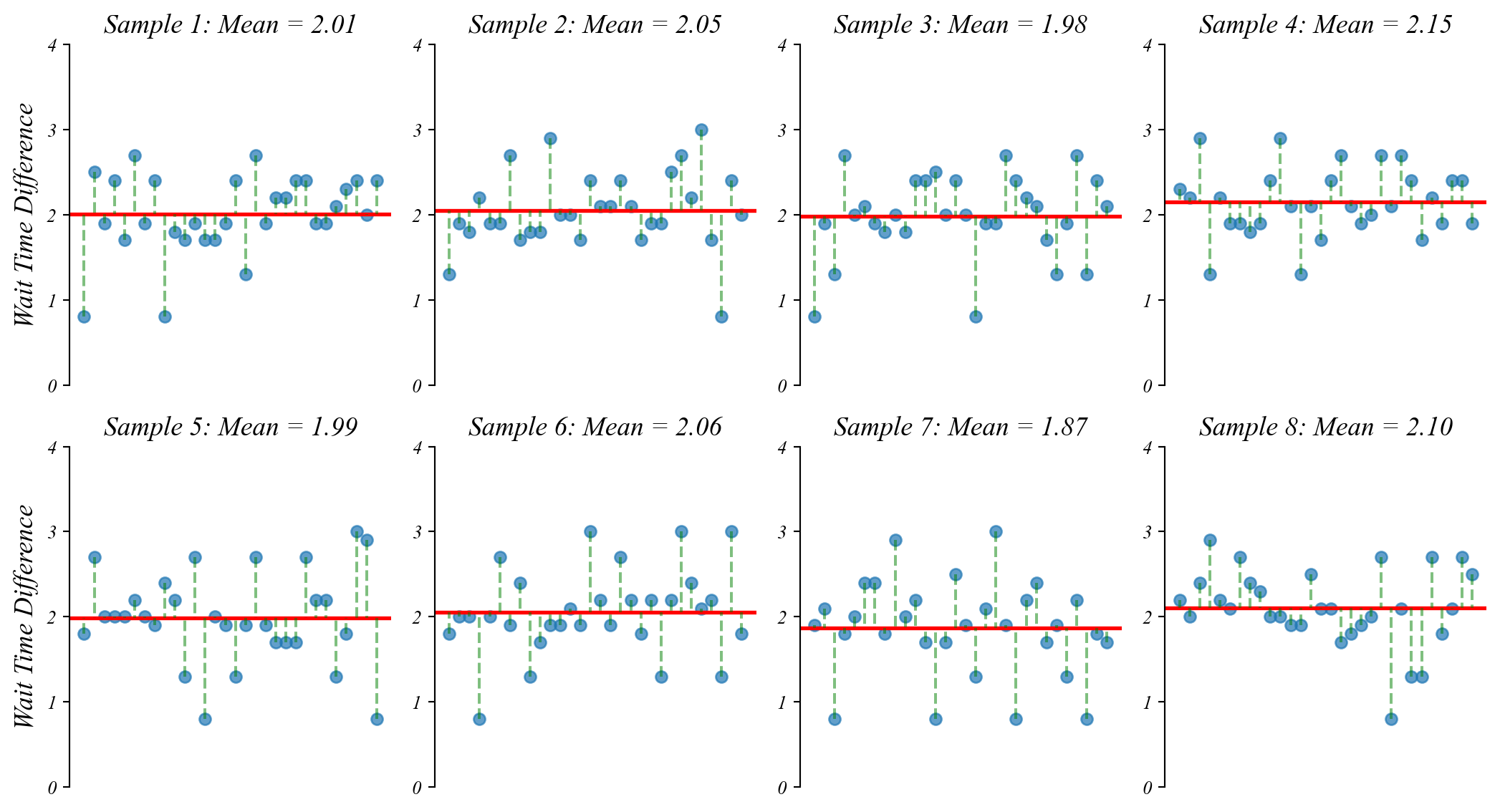
GLM: Sampling Error and Line Fitting

Like before, if we take many samples, we get slighly different means and slighly different fits.

GLM: Distribution Around the Sample Mean

The intercept terms follow a t-distribution centered on the true mean.

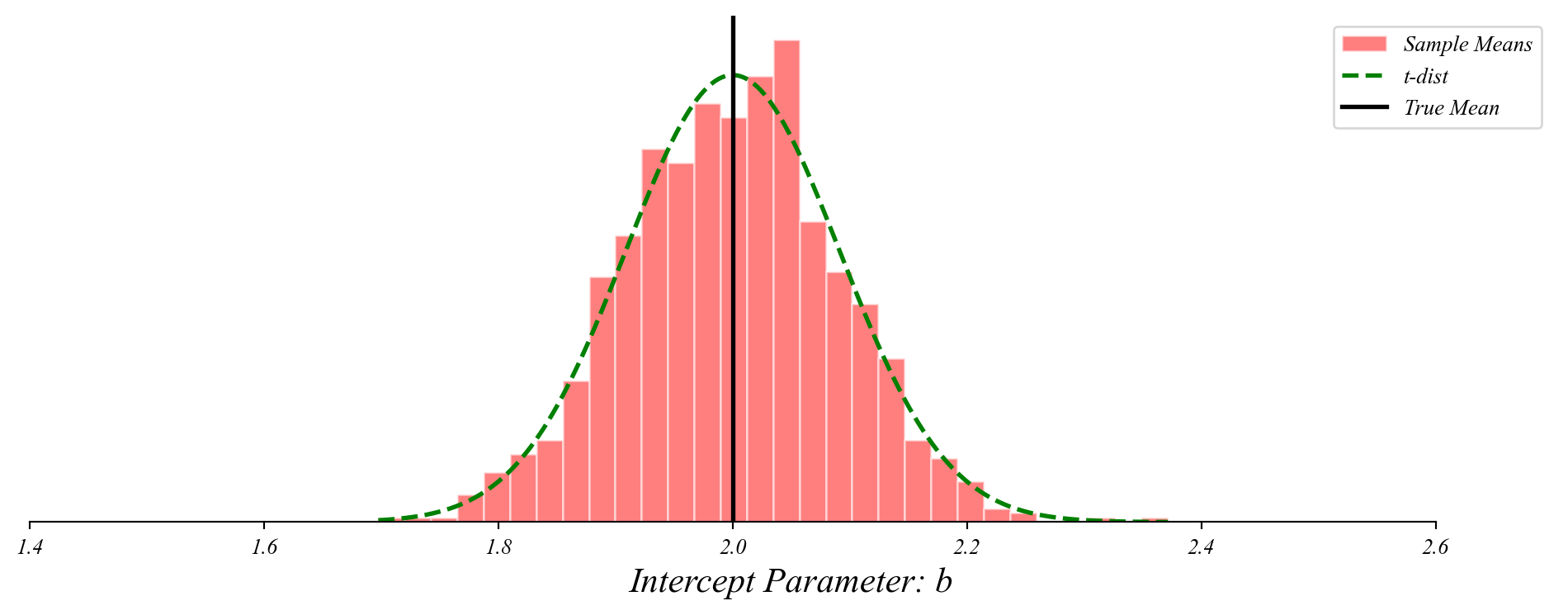
> we only observe one sample mean, so we center the distribution there

GLM: Distribution Around the Sample Mean

We center the sampling distribution on our observed sample mean.

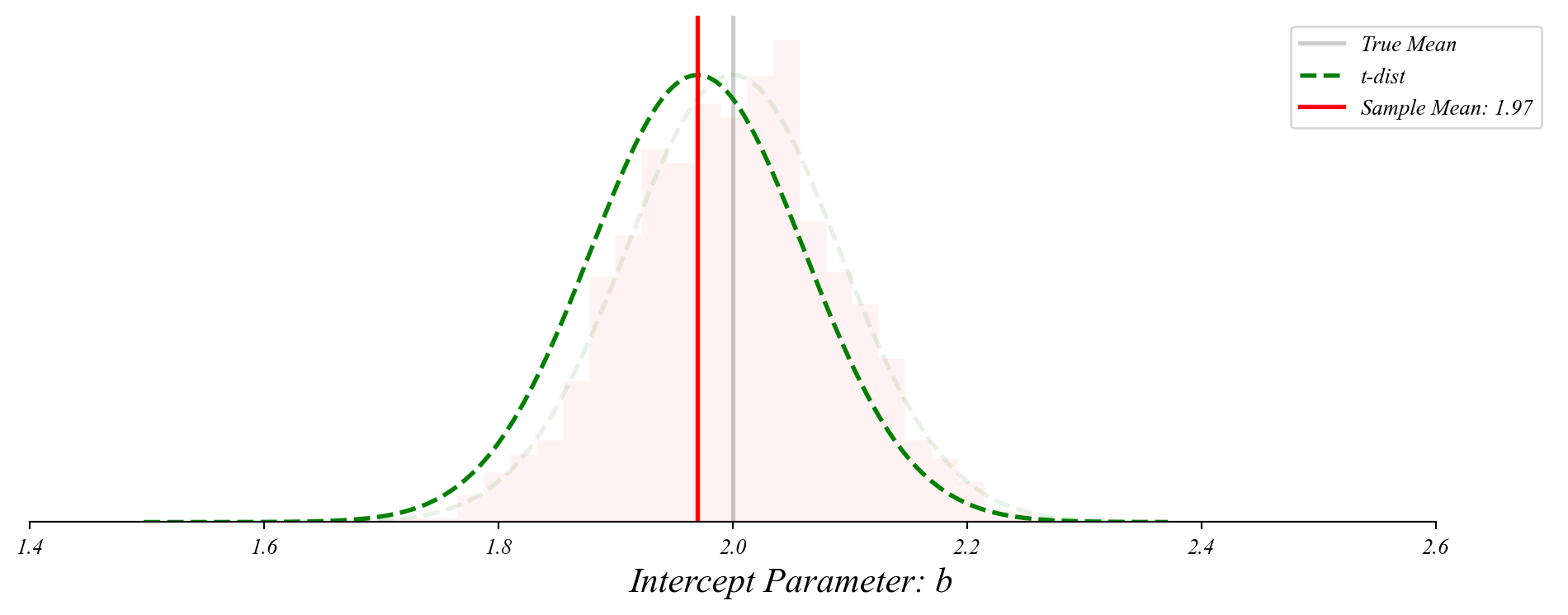
> what is the probability of seeing this if the average wait time is 1.8 minutes?

GLM: Finding p-values

The probability of something as extreme as our sample mean given the null.

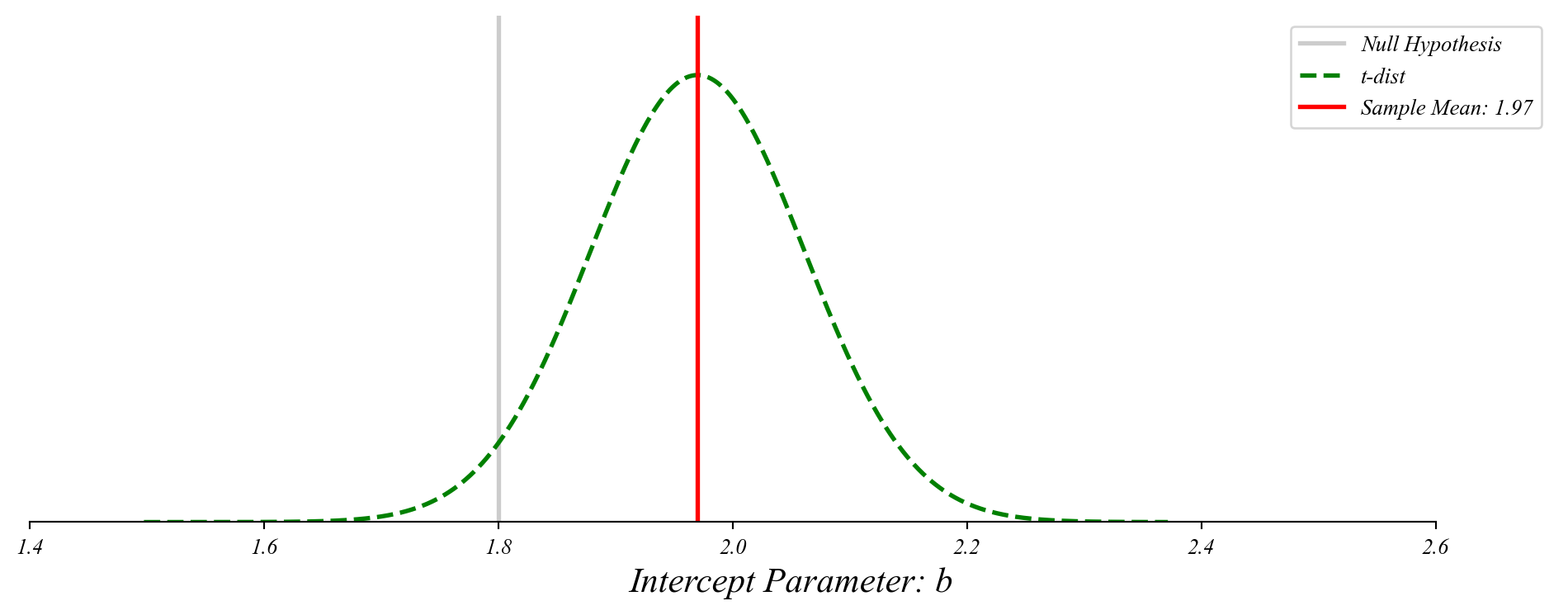
> here we’re centering the t-distribution on the observed sample mean

> as before, this is mathematically equivalent to centering on the null

GLM: Finding p-values

The probability of something as extreme as our sample mean given the null.

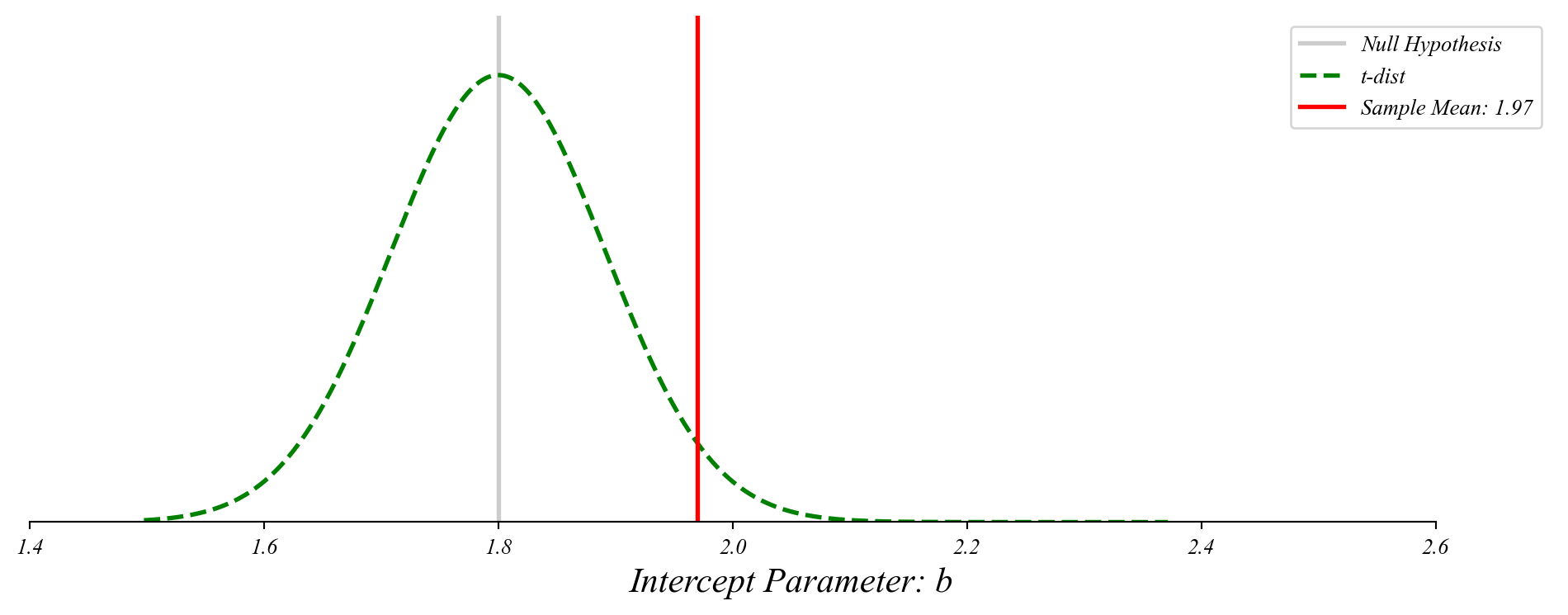
GLM: Finding p-values

The probability of something as extreme as our sample mean given the null.

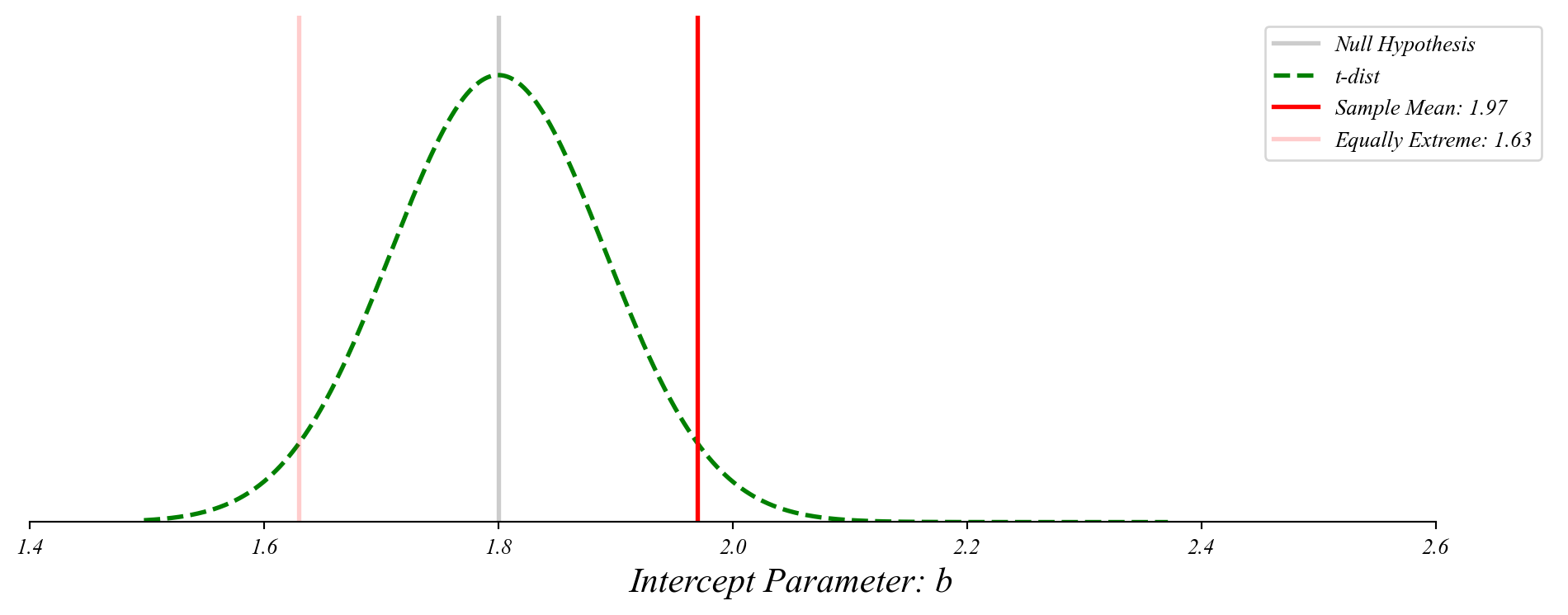
GLM: Finding p-values

The probability of something as extreme as our sample mean given the null.

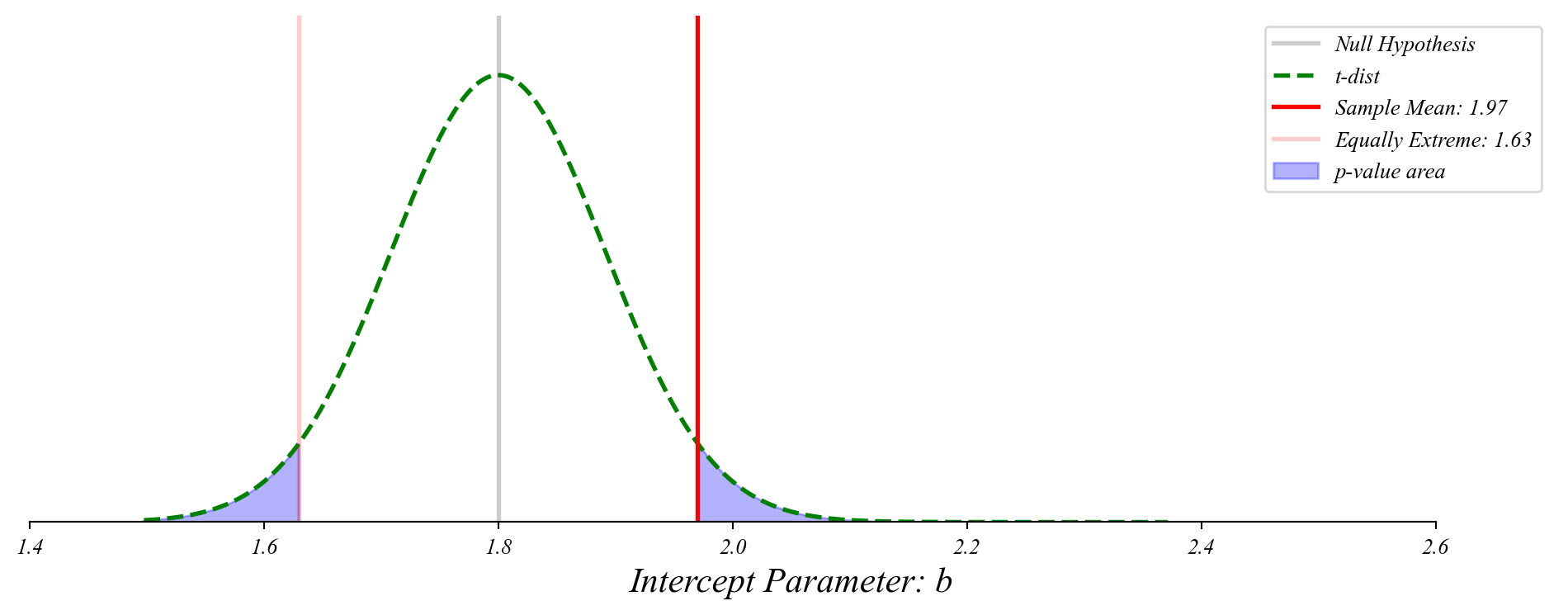
GLM: Intercept Model

A t-test is a linear model with only an intercept: \(y = \beta_0 + \epsilon\)

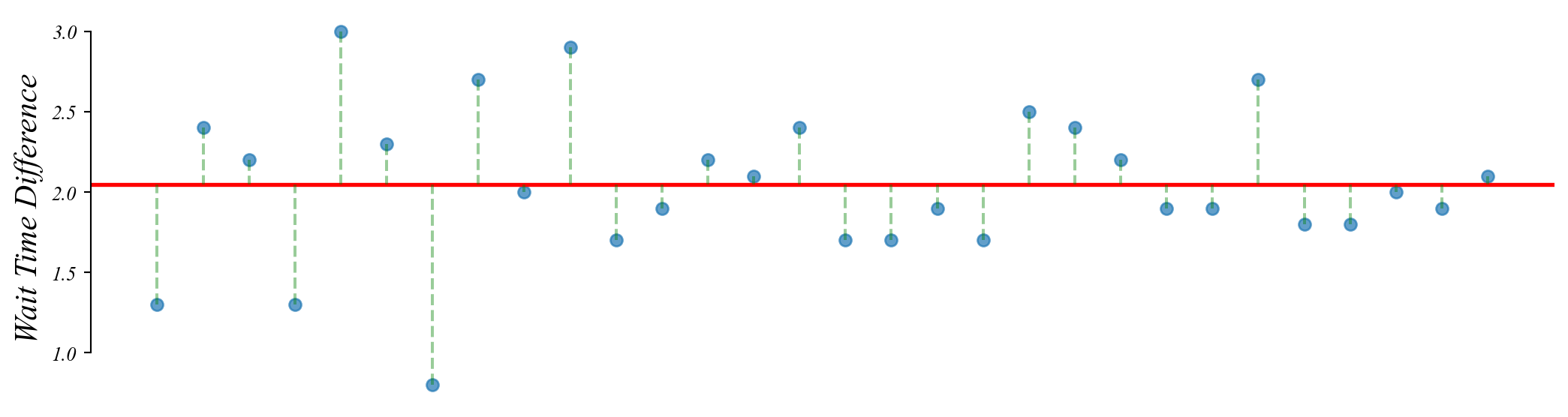
> the sample mean \(\beta_0\) minimizes the sum of squared errors

> the p-value tells us the probability of the data given the default null

> the best guess of the true mean is \(\beta_0\)

> this is the simplest version of an OLS regression model

Exercise 3.5 | Difference in Wait Times

Are wait times different in the morning and afternoon?

Looking Forward: Part 4

Bivariate General Linear Model

In Part 4 we will explore:

• Part 4.1 | Numerical Predictors
• Part 4.2 | Categorical Predictors
• Part 4.3 | Timeseries Models
• Part 4.4 | Causality

> all built on the same statistical foundation we explored today