ECON 0150 | Economic Data Analysis

The economist’s data analysis skillset.


Part 3.3 | Closeness: Sample / Population

A Big Question

How close are the sample mean (\(\bar{x}\)) and the population mean (\(\mu\))?



  • We found \(\bar{x}\) follows a normal distribution around \(\mu\).
  • How can we use this to learn about the population?
  • Lets systematize how “close” \(\bar{x}\) and \(\mu\) are.

Central Limit Theorem: Refresher

The sample mean follows a normal distribution around the true mean (\(\mu\)).

The standard deviation of the sample means is the standard error: \[SE = \frac{\sigma}{\sqrt{n}}\]

> as the sample size grows, the variability in sample means gets smaller

Example: Wait Times

\(\mu = 12\) and \(\sigma = 2.5\)

Smaller Sample Size: \(n = 30\)

Larger Sample Size: \(n = 200\)

Standard Error Mathematically

The standard error (SE) measures the precision of the estimate.

With \(n\) independent observations, each has a variance of \(\sigma^2\).

  1. The sum of \(n\) samples has variance \(n\sigma^2\):

\[VAR(a) + VAR(b) = VAR(a + b)\]

  1. Divide by \(n\) to find that the mean of \(n\) is \(\frac{\sigma^2}{n}\):

\[\frac{VAR\big(a\big)}{n} = VAR\Big(\frac{a}{n^2}\Big)\]

Therefore the standard error is \(\sqrt{\frac{\sigma^2}{n}} = \frac{\sigma}{\sqrt{n}}\).

Confidence Intervals: Known \(\sigma\)

If we know \(\sigma = 2.5\), we can calculate probabilities.

What’s the probability \(\bar{x}\) is within one standard error of \(\mu = 12\) with \(n=30\)?

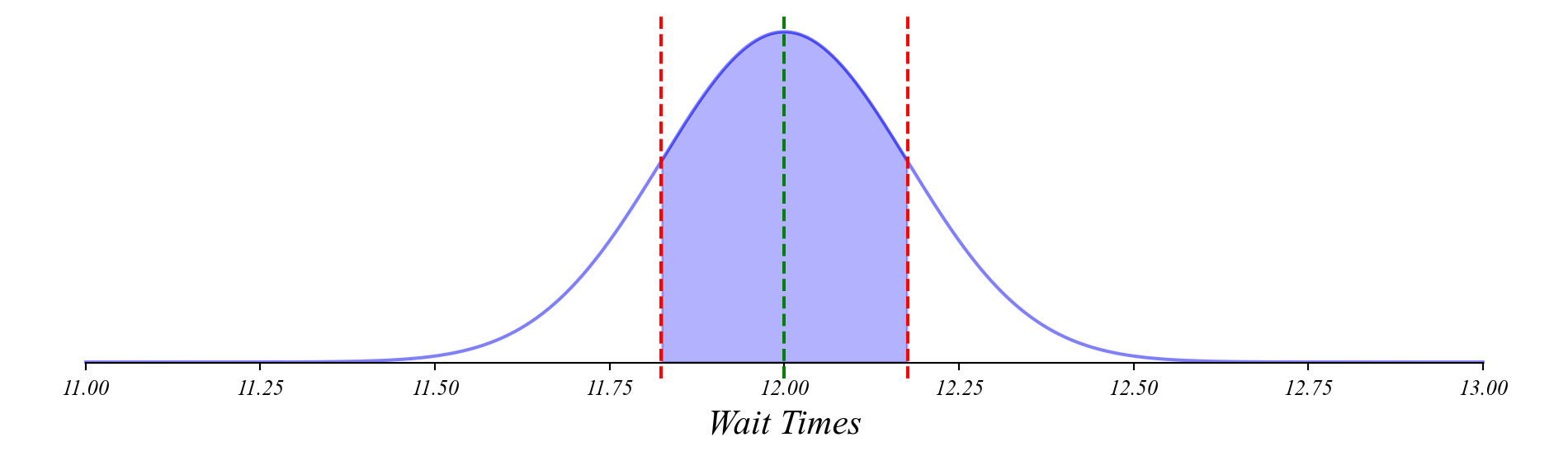
> \(P(\mu - SE \leq \bar{x} \leq \mu + SE) \approx 0.68\)

> so 68% of the time \(\bar{x}\) will fall within \([\mu - \frac{\sigma}{\sqrt{n}}, \mu + \frac{\sigma}{\sqrt{n}}]\)

> we call \([\mu - \frac{\sigma}{\sqrt{n}}, \mu + \frac{\sigma}{\sqrt{n}}]\) a 68% confidence interval

Exercise 3.3 | Confidence Intervals: Known \(\sigma\)

\(\mu = 12\) and \(\sigma = 2.5\) and \(n=30\)

Question: what’s the probability \(\bar{x}\) is closer than \(2\cdot SE\) to \(\mu\)?

se = sigma / np.sqrt(n)
probability = stats.norm.cdf(mu+2*se, loc=mean, scale=se) - stats.norm.cdf(mu-2*se, loc=mean, scale=se)

Exercise 3.3 | Simulating Confidence Intervals

Calculate the 95% confidence interval for waiting times.

Generate some sample data.

sample = np.random.normal(12, 2.5, 30)

Calculate sample statistics.

x_bar = np.mean(sample)
s = np.std(sample, ddof=1)
n = len(sample)
se = s / np.sqrt(n)

> if we took many samples, 95% of the time this interval would contain the truth

> we often just say: “we’re 95% confident the truth is in this interval”

Confidence Intervals: Unknown \(\sigma\)

What if we don’t know \(\sigma\) either?

> we used \(\bar{x}\) to estimate \(\mu\)

> can we use s to estimate \(\sigma\)?

> yes, but there’s a catch…

Using \(s\) Instead of \(\sigma\)

Sample standard deviation (\(s\)) has its own sampling variability.

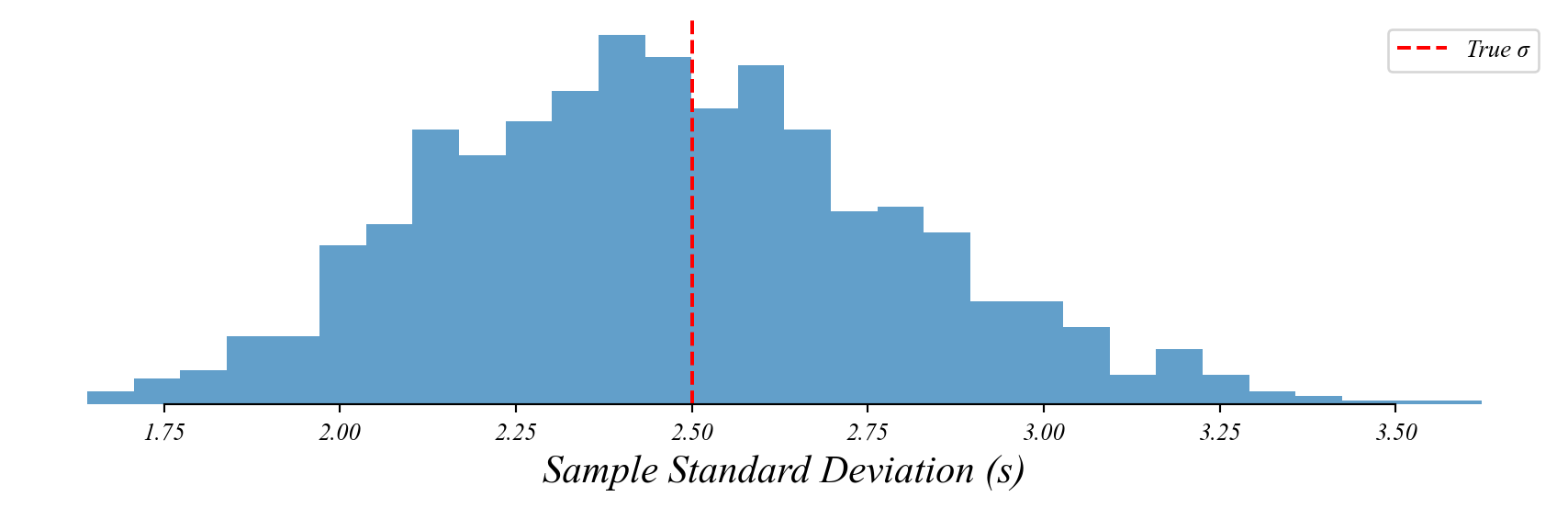
> this adds extra uncertainty to our interval

Normal vs t-Distribution

The t-distribution precisely accounts for the variation in \(s\) around \(\sigma\).

> \(\bar{x}\) follows a normal distribution with \(\mu\) and \(\sigma\)

> key insight: since \(s\) is random, using it instead \(\sigma\) introduces another r.v.

> this gives us the t-distribution with n-1 degrees of freedom

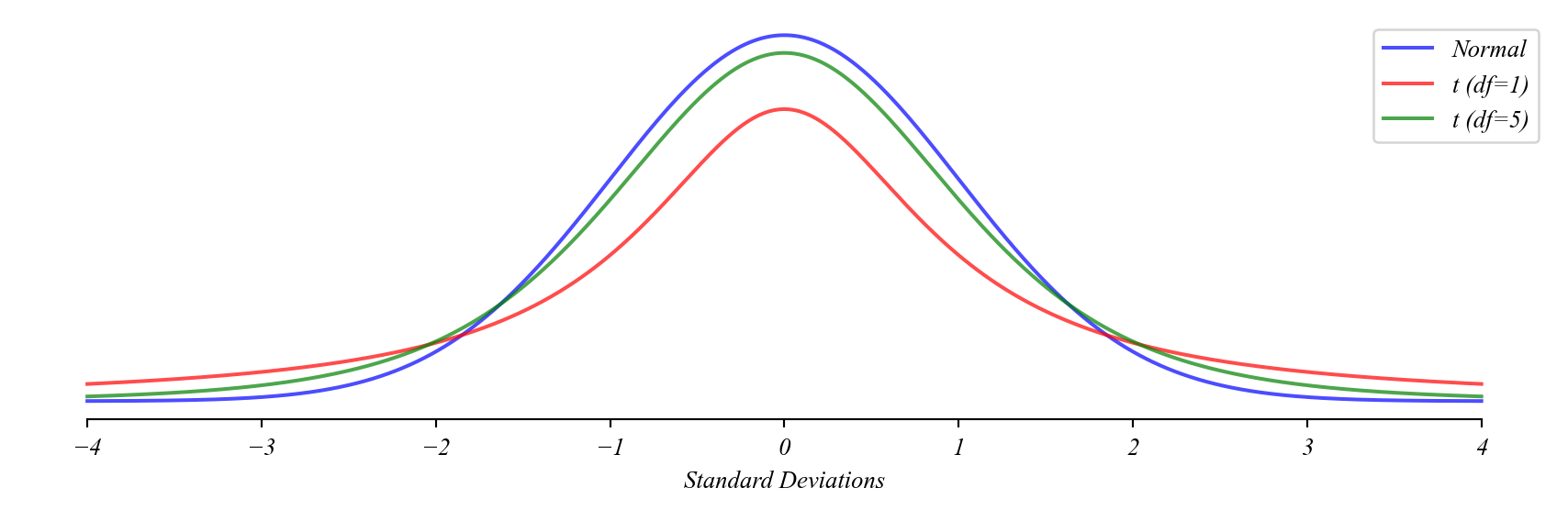
The t-Distribution

… acounts for the extra uncertainty in \(s\) around \(\sigma\).

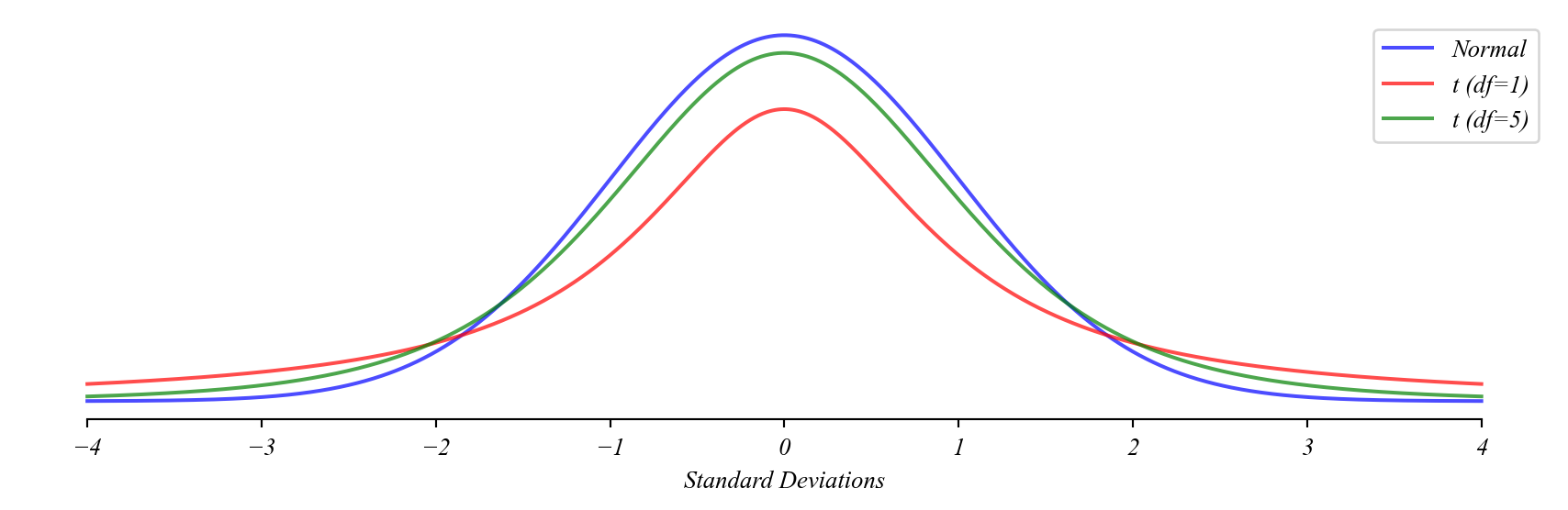
> t-distribution has heavier tails than normal

> approaches normal as sample size (\(n\)) increases

Exercise 3.3 | Normal vs t

The probability of closeness will be too large if we use the Normal instead of t.

Unknown \(\sigma\)

Now we can quantify our uncertainty about an unknown \(\mu\).

  1. \(\bar{x}\) follows a normal distribution around an unknown \(\mu\).
  1. Using \(s\) adds uncertainty, captured by t-distribution.
  1. We can use the t-distribution to make probability statements about \(\mu\).

Next Time: We’ll center the distribution on \(\bar{x}\) instead of \(\mu\) to develop a test of closeness.

Extra Questions

  1. How would the confidence interval change if we:

    • Increased sample size?
    • Wanted 99% confidence instead?
    • Had a more variable population?

  2. Why use t-distribution instead of normal?

  3. What does “95% confident” really mean?

  4. How could this help with economic decision-making?