ECON 0150 | Economic Data Analysis

The economist’s data analysis skillset.


Part 3.1 | Data vs the Population

Inferences From Data

What can we infer about those not in our data?



  • We’ve mastered summarizing data
  • But often we want to say something about the population, not just our data

Data Question 1: Sleep Time in Two Samples

Which group sleeps longer?

> everyone in Group A sleeps longer than anyone in Group B

Data Question 2: Sleep Time in Two Samples

Which group sleeps longer?

> these distributions overlap… lets compare them more precisely

Measures of Location

Where is the “center” of each group?


Mean: The average value \[\bar{x} = \frac{x_1 + x_2 + ... x_N}{N}\]

Measures of Location

Where is the “center” of each group?


Mean: The average value \[\bar{x} = \frac{1}{n}\sum_{i=1}^{n} x_i\]

# Calculate means
mean_A = group_A.mean()
mean_B = group_B.mean()
Group A mean: 7.14 hours
Group B mean: 6.98 hours

Data Question 2: Sleep Time in Two Samples

Which group sleeps longer? 

Group A mean: 7.14 hours
Group B mean: 6.98 hours

> group A sleeps longer on average

> but some in Group B sleep longer than most in Group A!

Measures of Dispersion

How spread out is the data?


Range: difference between the largest and smallest value in the data

  • Simple but doesn’t respond to changes near the middle of the distribution

Measures of Dispersion

How spread out is the data?


Mean Deviation: difference between each value and the average

\[ \sum \frac{x_i - \bar{x}}{n}\]

  • Simple but the average of the difference is zero…

Measures of Dispersion

How spread out is the data?


Mean Absolute Deviation: absolute value of the difference from the average

\[ \sum \frac{|x_i - \bar{x}|}{n}\]

  • The mean isn’t zero
  • A little more complex and isn’t so nice mathematically

Measures of Dispersion

How spread out is the data?


Variance: average squared difference from the mean

\[ Var_X = \sum \frac{(x_i - \bar{x})^2}{n}\]

  • Treats negatives appropriately
  • The mean isn’t zero
  • Mathematically nice
  • Units are uninformative

Measures of Dispersion

How spread out is the data?


Standard Deviation: A measure of spread \[S_X = \sqrt{\sum \frac{(x_i - \bar{x})^2}{n}}\]

  • Treats negatives appropriately
  • The mean isn’t zero
  • Mathematically nice
  • Units are roughly average deviation from the mean

Measures of Dispersion

How spread out is the data?


Standard Deviation: A measure of spread \[S_X = \sqrt{\sum \frac{(x_i - \bar{x})^2}{n}}\]

# Calculate standard deviations
std_A = group_A.std()
std_B = group_B.std()
Group A std dev: 1.50 hours
Group B std dev: 0.78 hours

> Group A has more variability - some sleep much less, some much more

Sample vs Population

Both groups are 50 people selected from two different counties.

Old question: “Which group sleeps longer?” (about the data)

New question: “Which county sleeps longer?” (about the population)

Sample vs Population

The data is a sample drawn from a population.

Sample vs Population

We observe samples but want to understand populations.



  • Data: 50 individuals we happened to sample from both counties
  • Population: All people who could live in these counties
    • Even if we surveyed everyone today, tomorrow would bring new residents
    • The population is a theoretical concept - an infinite pool of possibilities

Sample vs Population

What is data? A sample.

Random Variable: a random process about a population

  • the random variable is like a deck of cards

Probability (Mass/Density) Function: a function that assigns probabilities to each possible outcome

  • the probability function is like which cards are in the deck

Observation: a realization of a random variable . . .

  • the observation is the card you drew

Sample: a collection of observations

  • the sample is the record of cards you’ve drawn

Data is a Sample

A random variable generates our data.

Random Variable: a random process about a population

Probability Function: a function that assigns probabilities to each possibility

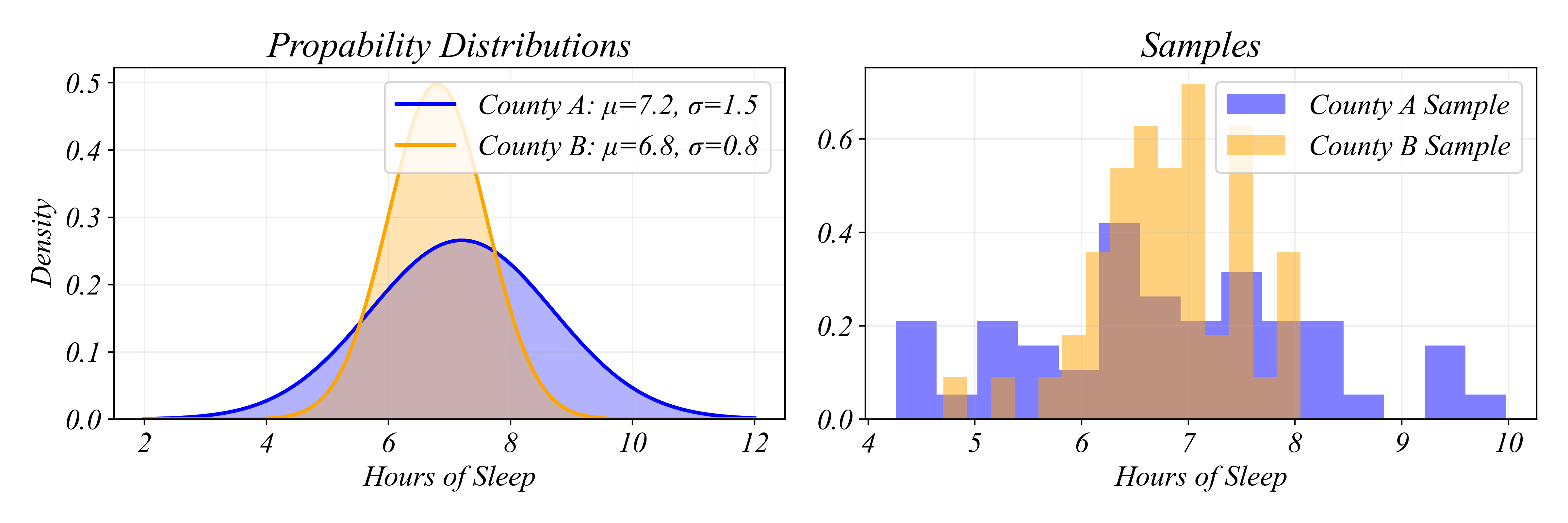
> data is a sample drawn from a random variable

Probability Functions

Random variables can have many kinds of probability functions.

Exercise 3.1 | Known Distribution

We can answer many kinds of probability questions when we know the distribution.

County A’s probability function:

\[x_i \sim N(μ=7.2, σ=1.5)\]

  1. What proportion of the population sleeps less than 5 hours?

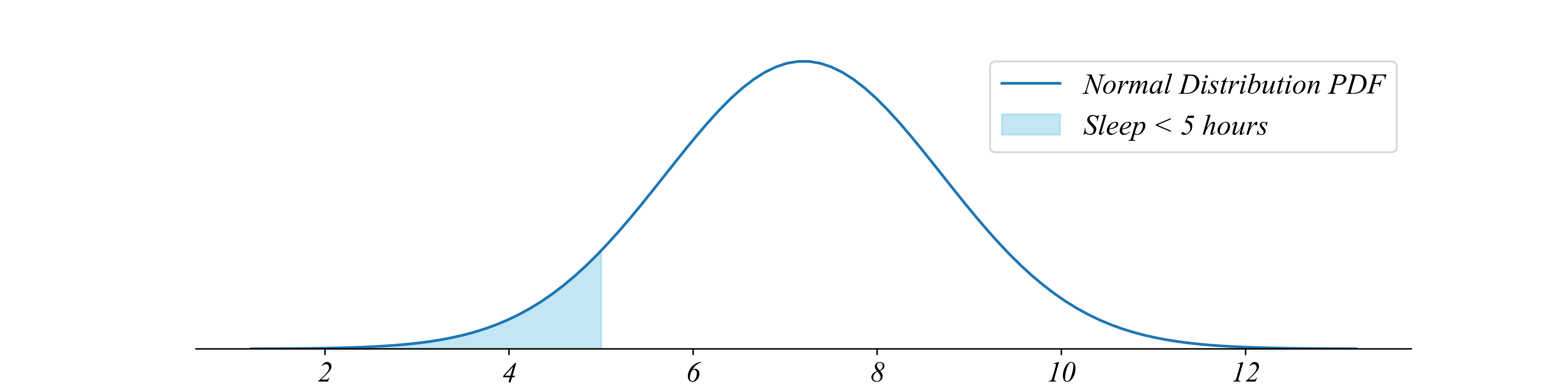
stats.norm.cdf(5, loc=mu, scale=sigma).item()

Exercise 3.1 | Known Distribution

We can answer many kinds of probability questions when we know the distribution.

County A’s probability function:

\[x_i \sim N(μ=7.2, σ=1.5)\]

  1. What proportion of the population sleeps more than 9 hours?

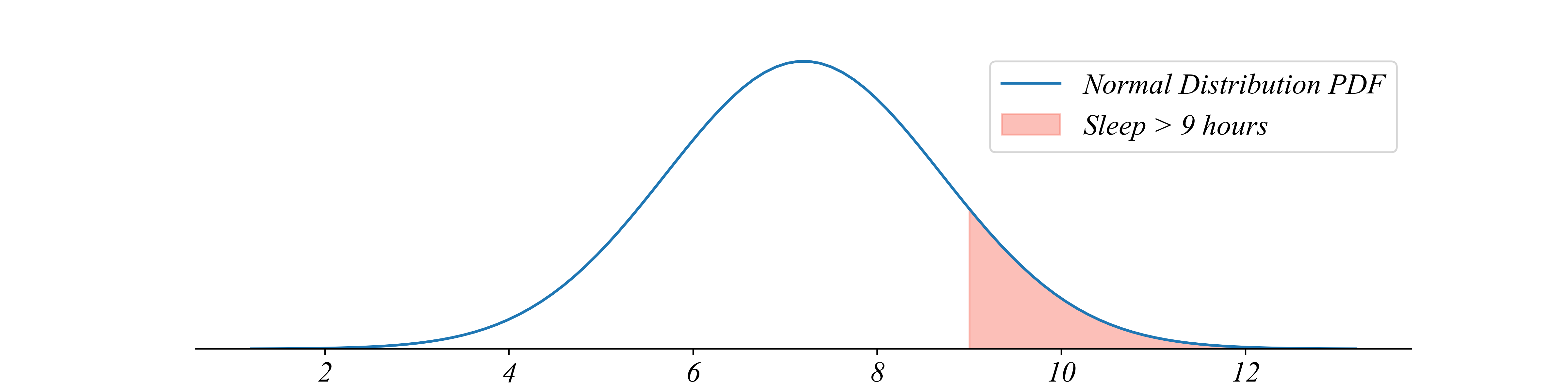
1 - stats.norm.cdf(9, loc=mu, scale=sigma).item()

Exercise 3.1 | Known Distribution

We can answer many kinds of probability questions when we know the distribution.

County A’s probability function:

\[x_i \sim N(μ=7.2, σ=1.5)\]

  1. How much sleep does the middle 92% of the population get?

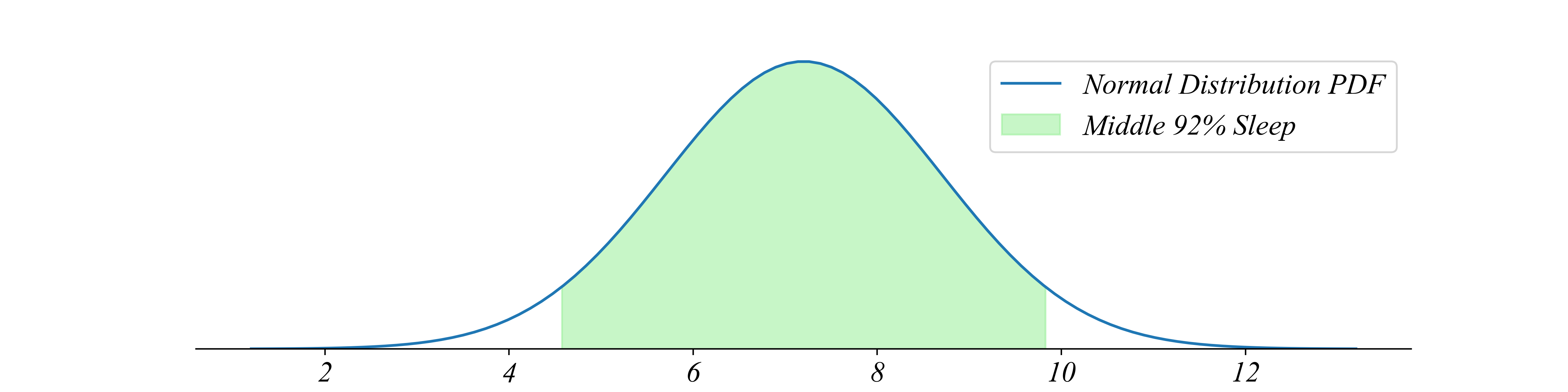
lower_bound = stats.norm.ppf(0.04, loc=mu, scale=sigma)
upper_bound = stats.norm.ppf(0.96, loc=mu, scale=sigma)

Unknown Distributions

What can we say about an unknown population if all see see is the sample?

What we observe:

  • Sample size: \(n = 50\)
  • Sample mean: \(\bar{x} = 7.24\) hours
  • Sample standard deviation: \(s = 1.48\) hours

What we want to know:

  • Population mean: \(\mu = ?\)
  • Population standard deviation: \(\sigma = ?\)
  • Population distribution: \(f(x) = ?\)

Unknown Distributions

What can we say about an unknown population if all see see is the sample?

The sample statistics (\(\bar{x}, S\)) are not the population parameters (\(\mu, \sigma\)).

\[\bar{x} \neq \mu\] \[s \neq \sigma\]

The Central Question

What can we say about an unknown population if all see see is the sample?



  • Part 3.2 | Central Limit Theorem - the distribution of the sample mean
  • Part 3.3 | Confidence Intervals - the closeness of the sample mean to the truth
  • Part 3.4 | Hypothesis Testing - the probability we are wrong


> we can answer questions about an unknown population using just a sample